Bài 17:
$a^2-2a(b+c)=b^2-2b(c+a)$
$\Leftrightarrow a^2-2ac=b^2-2bc$
$\Leftrightarrow (a^2-b^2)-(2ac-2bc)=0$
$\Leftrightarrow (a-b)(a+b-2c)=0$
$\Leftrightarrow a=b$ hoặc $a+b=2c$.
Nếu $a=b$. Thay vào đk $b^2-2b(c+a)=c^2-2c(a+b)$ thì:
$a^2-2a(c+a)=c^2-2c(a+a)$
$\Leftrightarrow -a^2-2ac=c^2-4ac$
$\Leftrightarrow a^2+c^2-2ac=0\Leftrightarrow (a-c)^2=0$
$\Leftrightarrow a=c$
Vậy $a=b=c\Rightarrow M=0$
Nếu $a+b=2c$
Khi đó ta có:
$a^2-2a(b+c)+b^2-2b(c+a)=2c^2-4c(a+b)$
$\Leftrightarrow a^2+b^2-4ab-2c(a+b)=2c^2-4c(a+b)$
$\Leftrightarrow (a+b)^2-6ab=2c^2-2c(a+b)=2c^2-2c.2c=-2c^2$
$\Leftrightarrow 4c^2-6ab=-2c^2$
$\Leftrightarrow 6ab=6c^2$
$\Leftrightarrow ab=c^2$
$\Leftrightarrow 4ab=4c^2=(2c)^2=(a+b)^2$
$\Leftrightarrow 4ab=a^2+b^2+2ab\Leftrightarrow (a-b)^2=0$
$\Leftrightarrow a=b$
Khi đó lại quay về TH1 và ta lại cm được $a=c$ nữa.
$\Rightarrow a=b=c\Rightarrow M=0$
Vậy $M=0$
Bài 18:
Đặt $\frac{a}{b-c}=x, \frac{b}{c-a}=y, \frac{c}{a-b}=z$.
Khi đó:
$xy+yz+xz=\frac{ab}{(b-c)(c-a)}+\frac{ac}{(b-c)(a-b)}+\frac{bc}{(c-a)(a-b)}=\frac{ab(a-b)+ac(a-c)+bc(b-c)}{(a-b)(b-c)(c-a)}=-1$
$N=(x+y+z)(\frac{1}{x}+\frac{1}{y}+\frac{1}{z})$
$=(x+y+z).\frac{xy+yz+xz}{xyz}=-\frac{x+y+z}{xyz}$
$=-[\frac{1}{xy}+\frac{1}{yz}+\frac{1}{xz}]$
$=-[\frac{(b-c)(c-a)}{ab}+\frac{(c-a)(a-b)}{bc}+\frac{(b-c)(a-b)}{ac}]$
$=-\frac{c(b-c)(c-a)+a(c-a)(a-b)+b(b-c)(a-b)}{abc}$
$=\frac{a^3+b^3+c^3-ab(a+b)-bc(b+c)-ac(a+c)+3abc}{abc}$
$=\frac{a^3+b^3+c^3-ab(-c)-bc(-a)-ac(-b)-3abc}{abc}$
$=\frac{a^3+b^3+c^3+6abc}{abc}$
$=\frac{(a+b)^3-3ab(a+b)+c^3+6abc}{abc}=\frac{(-c)^3-3ab(-c)+c^3+6abc}{abc}$
$=\frac{-c^3+3abc+c^3+6abc}{abc}=\frac{9abc}{abc}=9$

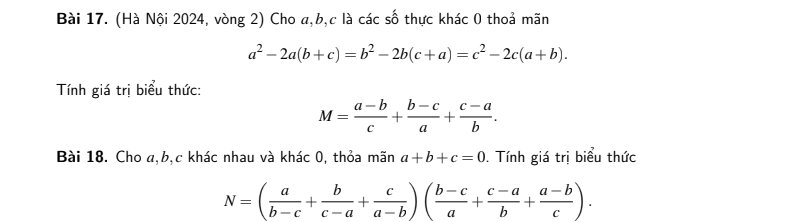











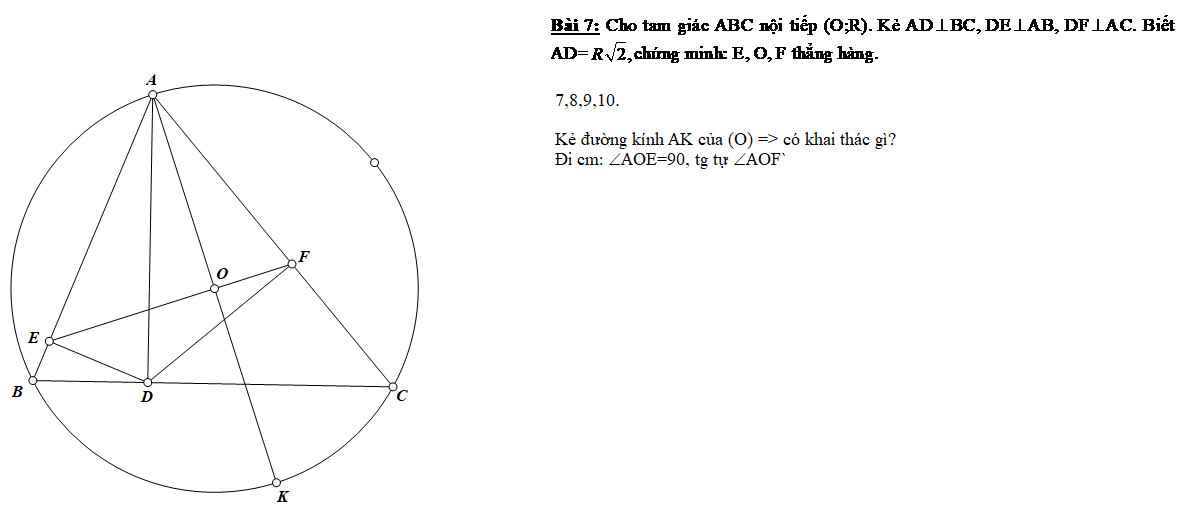



 em cần giải gấp bài 2 ạ, mọi người giúp em với ạ
em cần giải gấp bài 2 ạ, mọi người giúp em với ạ




