Lời giải:
ĐKXĐ: $x>0$. Áp dụng BĐT AM-GM:
\(M=PQ-\sqrt{x}=\frac{\sqrt{x}-1}{\sqrt{x}+1}.\frac{2(x-1)}{\sqrt{x}}-\sqrt{x}=\frac{2(\sqrt{x}-1)^2(\sqrt{x}+1)}{\sqrt{x}(\sqrt{x}+1)}-\sqrt{x}\)
\(=\frac{2(\sqrt{x}-1)^2}{\sqrt{x}}-\sqrt{x}=\sqrt{x}+\frac{2}{\sqrt{x}}-4\\ \geq 2\sqrt{\sqrt{x}.\frac{2}{\sqrt{x}}}-4=2\sqrt{2}-4\)
Vậy $M_{\min}=2\sqrt{2}-4$













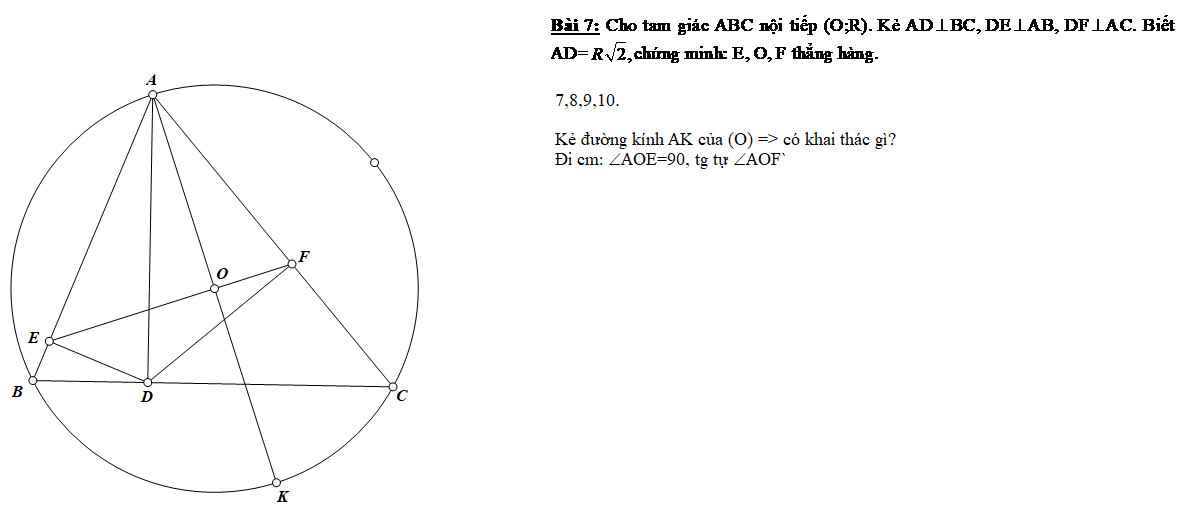



 em cần giải gấp bài 2 ạ, mọi người giúp em với ạ
em cần giải gấp bài 2 ạ, mọi người giúp em với ạ




