Question

Mọi người giúp em từ câu 20-25 với ạ, chi tiết càng tốt ạ, em cảm ơn!!!

Answer 1

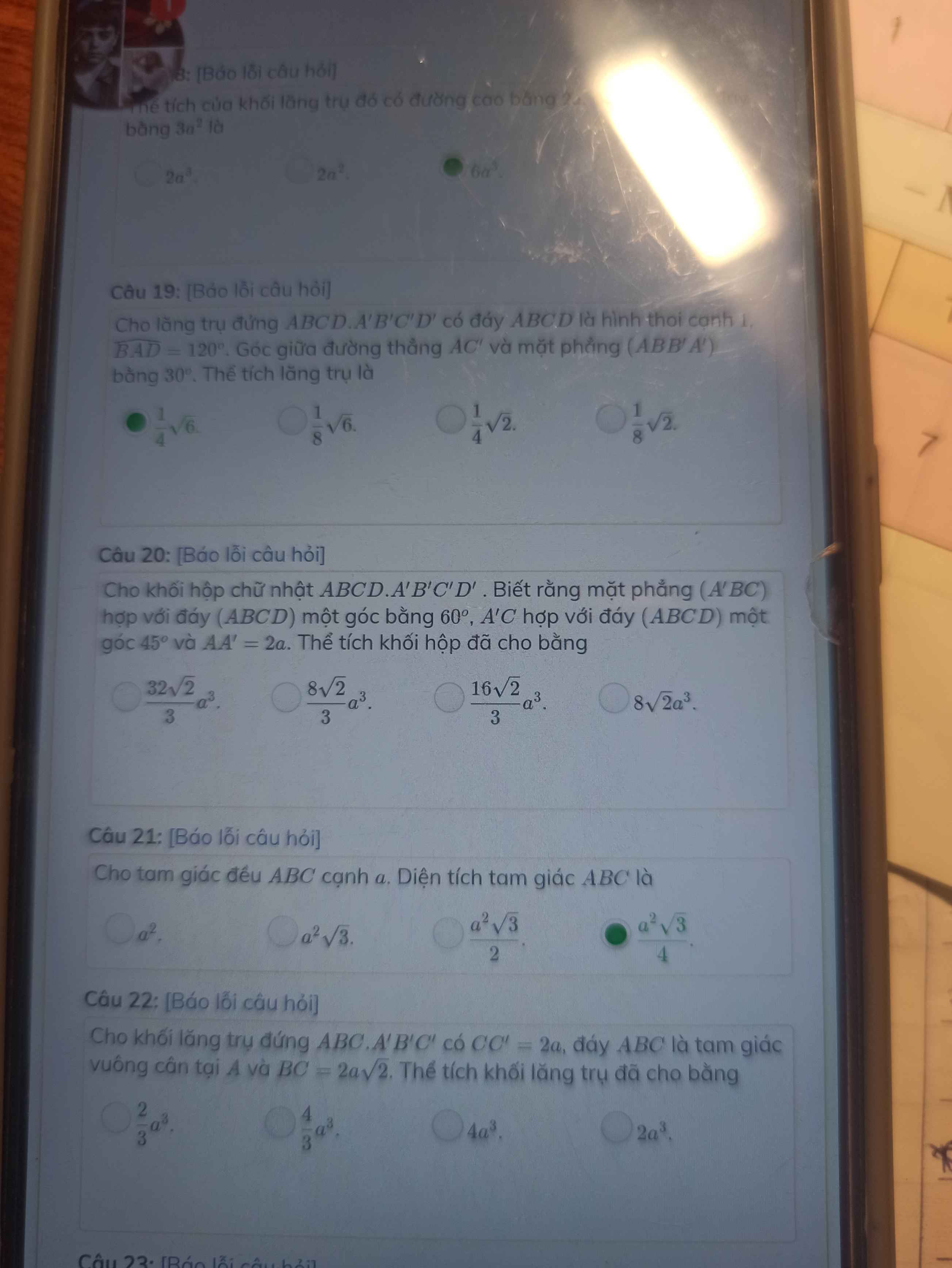
Câu 20:

Kẻ $SH\perp AB$. Mà $AB$ là giao tuyến của 2 mp vuông góc $(SAB)$ và $(ABCD)$ nên $SH\perp (ABCD)$

Vì $SAB$ đều nên $SH=\frac{\sqrt{3}}{2}AB=\frac{\sqrt{3}}{2}a$

$S_{ACD}=\frac{AB.AD}{2}=\frac{a.2a}{2}=a^2$
Do đó:

$V_{S.ACD}=\frac{1}{3}.SH.S_{ACD}=\frac{1}{3}.\frac{\sqrt{3}}{2}a.a^2=\frac{\sqrt{3}}{6}a^3$
Đáp án D.

Answer 2

Câu 21:
Do tam giác $ABC$ vuông cân tại $B$ nên $AB=BC=\frac{AC}{\sqrt{2}}=\frac{a}{\sqrt{2}}$

$SA\perp (ABC)\Rightarrow \angle (SB, (ABC))=\angle (SB, AB)=\widehat{SBA}=60^0$

$\tan \widehat{SBA}=\frac{SA}{AB}$

$\Rightarrow SA=\tan \widehat{SBA}.AB=\tan 60^0.\frac{a}{\sqrt{2}}=\frac{\sqrt{6}}{2}a$

Thể tích $V_{S.ABC}=\frac{1}{3}SA.S_{ABC}$
$=\frac{1}{3}.\frac{\sqrt{6}}{2}a.\frac{\frac{a}{\sqrt{2}}.\frac{a}{\sqrt{2}}}{2}=\frac{a^3\sqrt{6}}{24}$ 

Đáp án A.

Answer 3

Câu 22:
Vì $(SAB), (SAC)$ cùng vuông góc với $(ABC)$ mà $(SAB)\cap (SAC)\equiv SA$ nên $SA\perp (ABC)$

Áp dụng định lý Pitago cho tam giac $SAC$ vuông tại $A$:

$SA=\sqrt{SC^2-AC^2}=\sqrt{3a^2-a^2}=\sqrt{2}a$
$S_{ABC}=\frac{\sqrt{3}}{4}a^2$ do $ABC$ là tg đều cạnh $a$

$V_{S.ABC}=\frac{1}{3}SA.S_{ABC}=\frac{1}{3}.\sqrt{2}a.\frac{\sqrt{3}}{4}a^2=\frac{\sqrt{6}}{12}a^3$

Đáp án B.

Answer 4

Câu 24:

Vì $SA\perp (ABCD)$ nên $\angle (SD, (ABCD))=\angle (SD, AD)=\widehat{SDA}=30^0$

$\frac{SA}{AD}=\tan \widehat{SDA}$

$\Rightarrow SA=AD.\tan \widehat{SDA}=a.\tan 30^0=\frac{\sqrt{3}}{3}a$

$V_{S.ABCD}=\frac{1}{3}.SA.S_{ABCD}=\frac{1}{3}.\frac{\sqrt{3}}{3}a.a^2=\frac{\sqrt{3}}{9}a^3$

Đáp án D.

Answer 5

Câu 23:

Vì $ABCD$ là hình vuông nên $AB\parallel CD$

$\Rightarrow d(SB, CD)=d((SAB), CD)=d(D, (SAB))=DA=a$

Đáp án B.

Answer 6

Câu 25:

Chiều cao của khối chóp là: $h=3\sin 60^0=\frac{3\sqrt{3}}{2}$ (cm)

Diện tích đáy: $\frac{\sqrt{3}}{4}.6^2=9\sqrt{3}$ (cm vuông)

Thể tích khối chóp:

$V=\frac{1}{3}.\frac{3\sqrt{3}}{2}.9\sqrt{3}=\frac{27}{2}$ (cm khối)

Đáp án B.