5c.
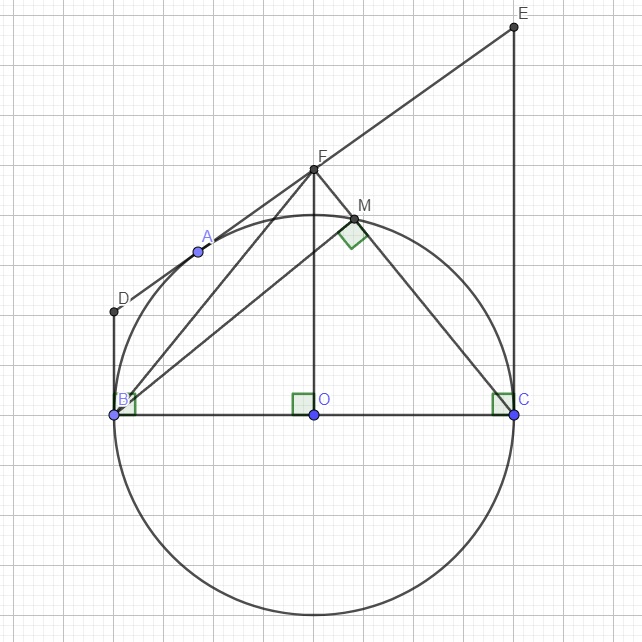
DB song song CE (cùng vuông góc BC) nên BCED là hình thang vuông tại B và C
O, F lần lượt là trung điểm BC, DE \(\Rightarrow OF\) là đường trung bình hình thang BCED
\(\Rightarrow OF||DB\Rightarrow OF\perp BC\)
Trong tam giác FBC, OF vừa là đường cao vừa là trung tuyến nên tam giác FBC cân tại F
\(\Rightarrow BF=CF\)
Lại có BC là đường kính nên \(\widehat{BMC}=90^0\) (góc nt chắn nửa đường tròn)
Xét 2 tam giác BMC và FOC có:
\(\left\{{}\begin{matrix}\widehat{BMC}=\widehat{FOC}=90^0\\\widehat{BCF}-chung\end{matrix}\right.\)
\(\Rightarrow\Delta BMC\sim\Delta FOC\left(g.g\right)\)
\(\Rightarrow\dfrac{MC}{OC}=\dfrac{BC}{CF}\)
\(\Rightarrow MC.BF=MC.CF=OC.BC=R.2R=2R^2\)
Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.
