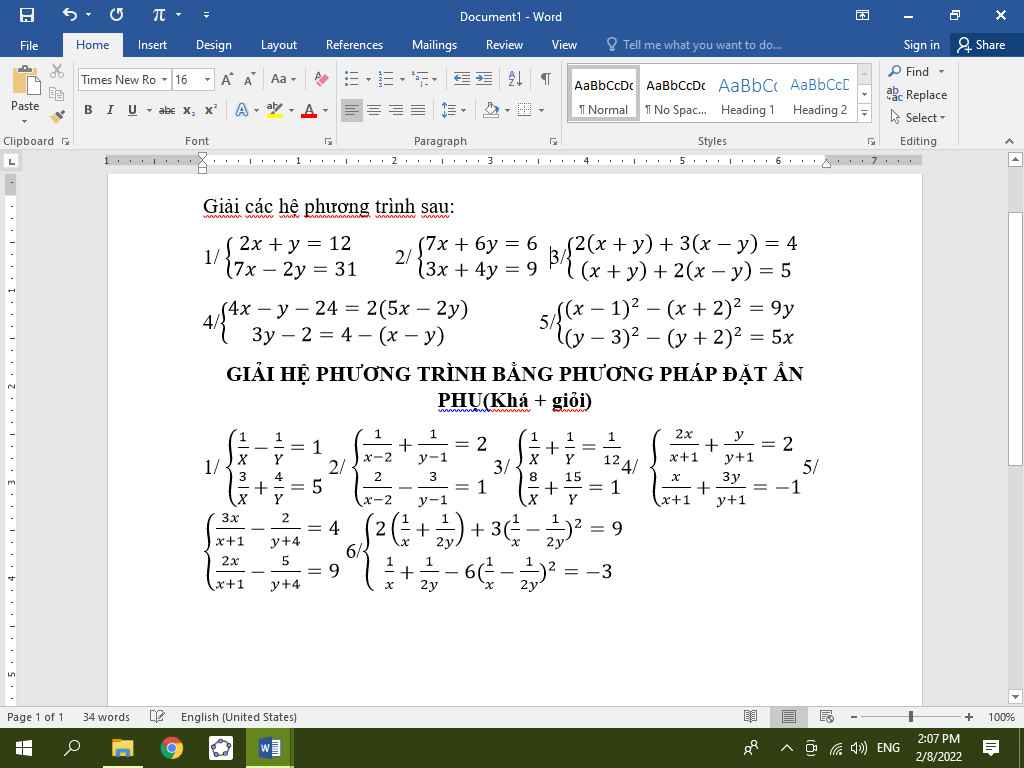
Câu này giải kiểu lớp 9 hơi tốn thời gian do ít công cụ.
Pt hoành độ giao điểm:
\(\dfrac{1}{2}x^2=x+4\Leftrightarrow x^2-2x-8=0\Rightarrow\left[{}\begin{matrix}x=-2\Rightarrow y=2\\x=4\Rightarrow y=8\end{matrix}\right.\)
\(\Rightarrow A\left(-2;2\right)\) ; \(B\left(4;8\right)\)
Gọi C là giao điểm của AB (hay d) với trục Ox \(\Rightarrow C\left(-4;0\right)\)
Gọi D, E lần lượt là hình chiếu của A, B lên Ox \(\Rightarrow D\left(-2;0\right);E\left(4;0\right)\)
ABED tạo thành hình thang vuông tại D và E với \(AD=\left|y_A\right|=2\) ; \(BE=\left|y_B\right|=8\); \(DE=\left|x_B-x_A\right|=6\), \(OD=\left|x_D\right|=2\) ; \(OE=\left|x_E\right|=4\)
\(S_{OAB}=S_{ABED}-\left(S_{OAD}+S_{OBE}\right)\)
\(=\dfrac{1}{2}\left(AD+BE\right).DE-\left(\dfrac{1}{2}AD.OD+\dfrac{1}{2}BE.OE\right)=12\)
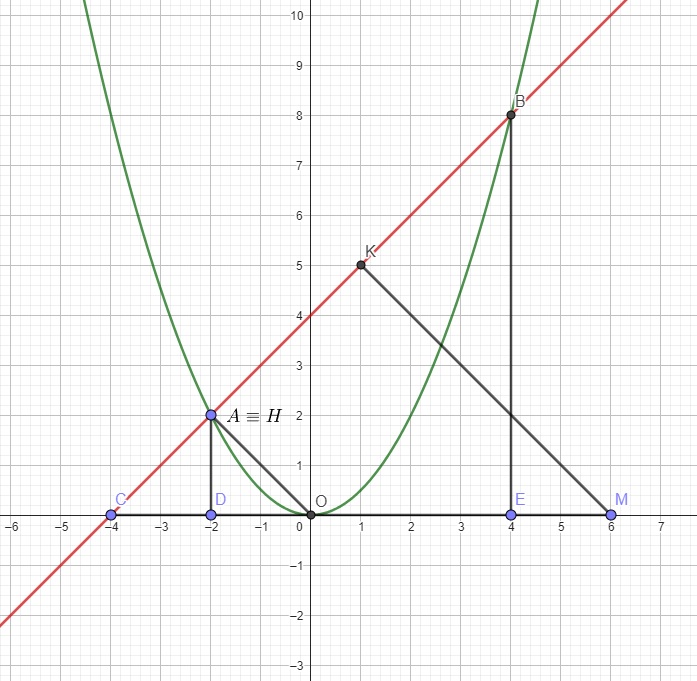
Từ O kẻ OH vuông góc AB, từ M kẻ MK vuông góc AB
Ta có:
\(\dfrac{S_{MAB}}{S_{OAB}}=\dfrac{30}{12}=\dfrac{15}{6}=\dfrac{\dfrac{1}{2}MK.AB}{\dfrac{1}{2}OH.AB}=\dfrac{MK}{OH}\)
Mặt khác, do OH song song MK (cùng vuông AB), áp dụng định lý Thales:
\(\dfrac{OH}{MK}=\dfrac{CO}{CM}=\dfrac{\left|x_O-x_C\right|}{\left|x_M-x_C\right|}=\dfrac{4}{\left|x_M+4\right|}=\dfrac{4}{x_M+4}\) (do M thuộc tia Ox nên \(x_M>0\))
\(\Rightarrow\dfrac{4}{x_M+4}=\dfrac{6}{15}\) \(\Rightarrow x_M=6\)
\(\Rightarrow M\left(6;0\right)\)
Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.
