2)\(\dfrac{x-3}{2}+2< \dfrac{2x+1}{3}\Leftrightarrow\dfrac{x+1}{2}< \dfrac{2x+1}{3}\Leftrightarrow0< \dfrac{2x+1}{3}-\dfrac{x+1}{2}=\dfrac{x-1}{6}\Leftrightarrow x-1< 0\Leftrightarrow x< 1\)
Vậy x < 1.
Bài 2:
a)ĐKXĐ:x ≠ 0,1
b)Ta có \(A=\left(\dfrac{\left(x+1\right)\left(1-x\right)-x}{x\left(1-x\right)}+\dfrac{2-x^2}{x^2-x}\right).\dfrac{\left(x-1\right)^2}{x\left(x+1\right)}=\left(\dfrac{\left(x+1\right)\left(x-1\right)+x}{x\left(x-1\right)}+\dfrac{2-x^2}{x^2-x}\right).\dfrac{\left(x-1\right)^2}{x\left(x+1\right)}=\left(\dfrac{x^2-1+x+2-x^2}{x\left(x-1\right)}\right).\dfrac{\left(x-1\right)^2}{x\left(x+1\right)}=\dfrac{x+1}{x\left(x-1\right)}.\dfrac{\left(x-1\right)^2}{x\left(x+1\right)}=\dfrac{x-1}{x^2}\)
Vì |x - 1| = 2 <=> x - 1 = 2,-2 <=> x ∈ {3,-1}
Thay vào, ta có A ∈ {2/9, -2}
c) Từ câu b, ta có A = x - 1/x^2, do đó A ≤ 1/4 <=> x - 1/x^2 ≤ 1/4 <=> 4x - 4/x^2 ≤ 1 <=> 4x - 4/x^2 - 1 ≤ 0 <=> 4x - 4 - x^2/x^2 ≤ 0 <=> -(x - 2)^2/x^2 ≤ 0 (luôn đúng)
Vậy ta có đpcm







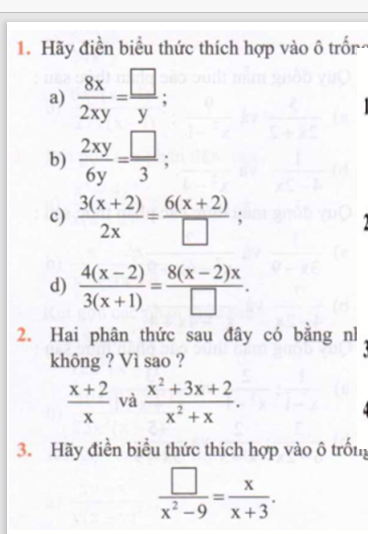 Mọi người giải giúp em với ạ em đang cần gấp ạ
Mọi người giải giúp em với ạ em đang cần gấp ạ mọi người giải giúp em bài này với ạ em đang cần gấp ạ
mọi người giải giúp em bài này với ạ em đang cần gấp ạ




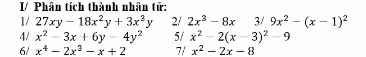



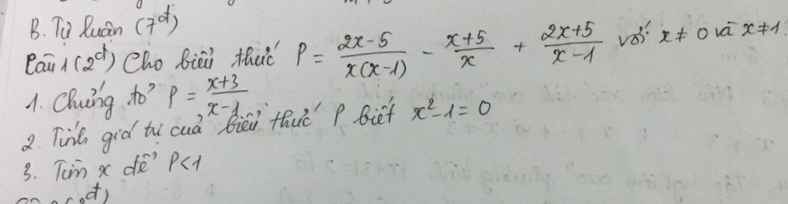 mọi người giúp em với ạ , em đang cần gấp :))
mọi người giúp em với ạ , em đang cần gấp :))


