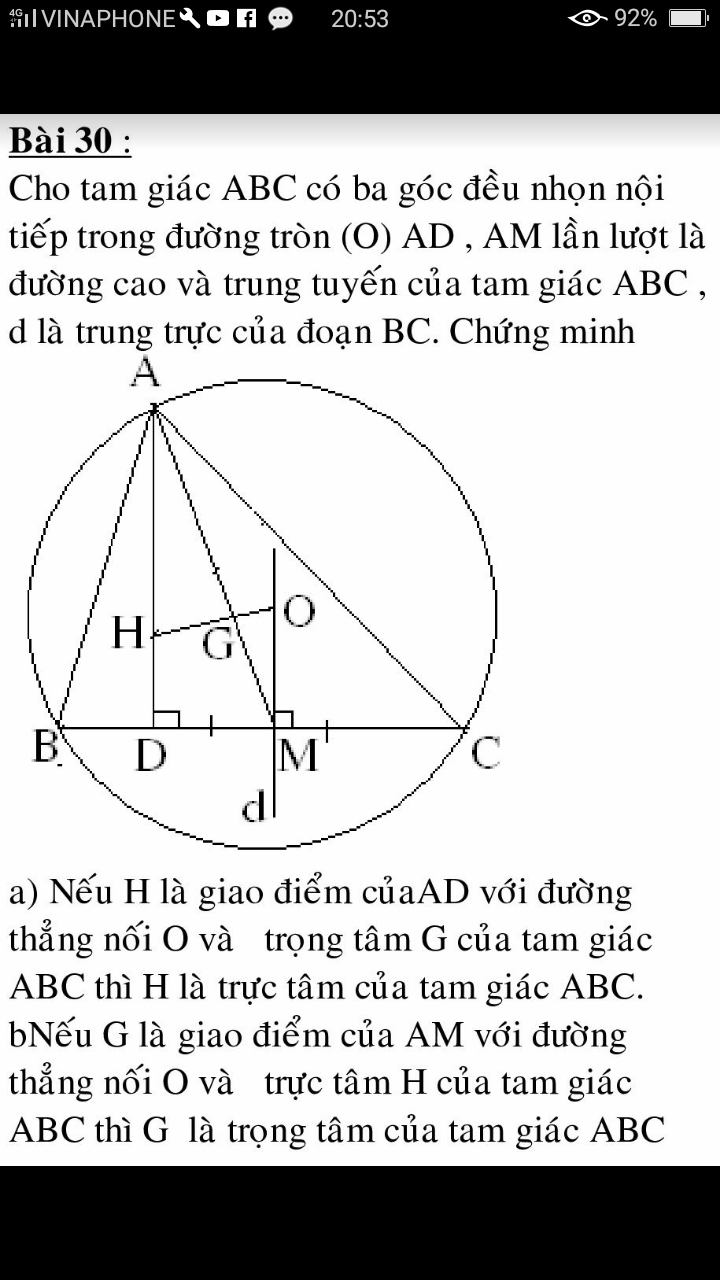
1: Xét tứ giác DHEC có \(\widehat{HDC}+\widehat{HEC}=90^0+90^0=180^0\)
nên DHEC là tứ giác nội tiếp
2: ΔOBC cân tại O
mà OI là đường cao
nên I là trung điểm của BC
Xét ΔABC có
AD,BE là các đường cao
AD cắt BE tại H
Do đó: H là trực tâm của ΔBAC
=>CH\(\perp\)AB
Xét (O) có
ΔABM nội tiếp
AM là đường kính
Do đó: ΔABM vuông tại B
=>BA\(\perp\)BM
mà CH\(\perp\)BA
nên CH//BM
Xét (O) có
ΔACM nội tiếp
AM là đường kính
Do đó: ΔACM vuông tại C
=>AC\(\perp\)CM
mà BH\(\perp\)AC
nên BH//CM
Xét tứ giác BHCM có
BH//CM
BM//CH
Do đó: BHCM là hình bình hành
=>BC cắt HM tại trung điểm của mỗi đường
mà I là trung điểm của BC
nên I là trung điểm của HM






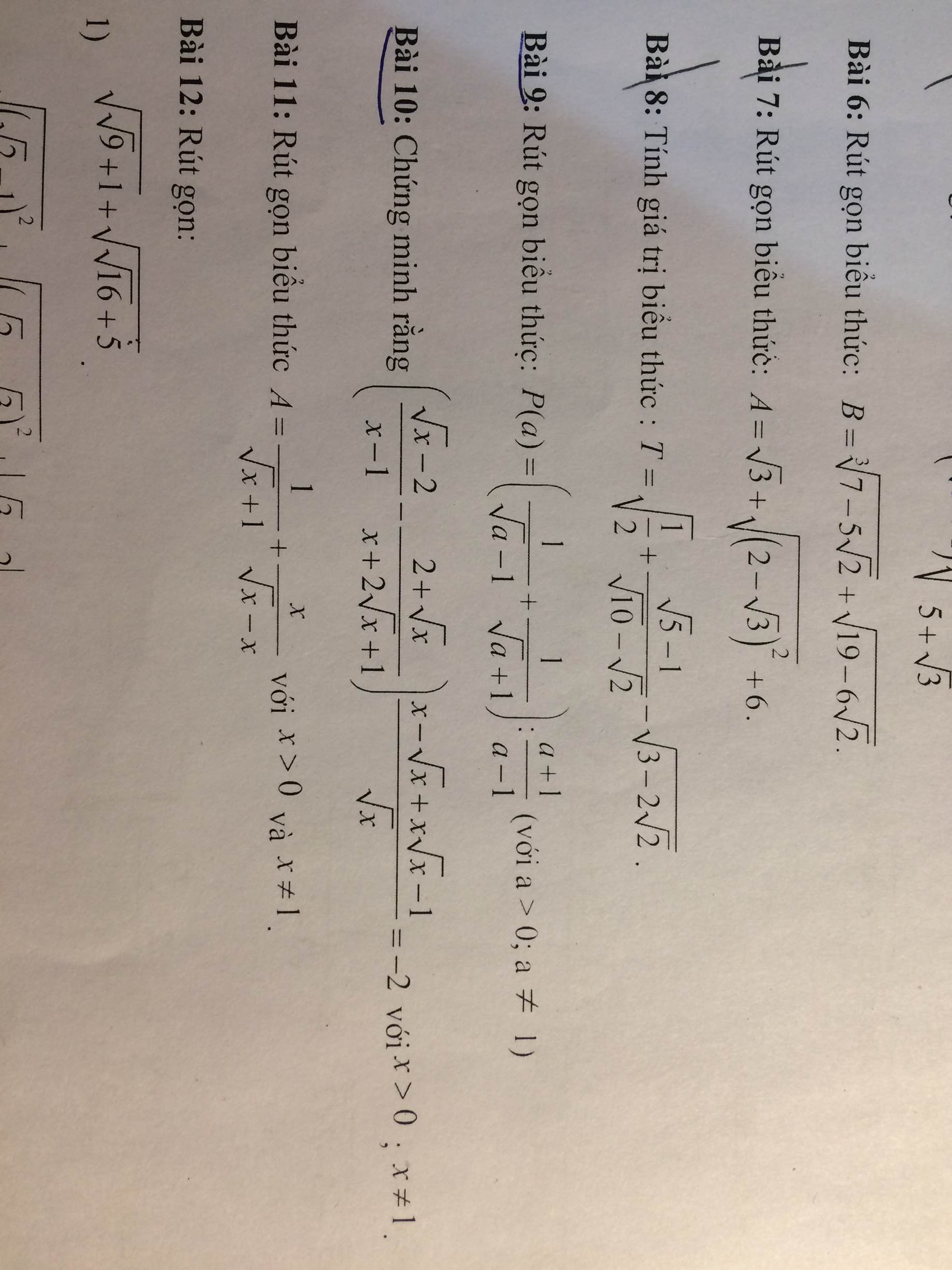






 mọi người giúp mik bài 4 câu a vs ạ
mọi người giúp mik bài 4 câu a vs ạ