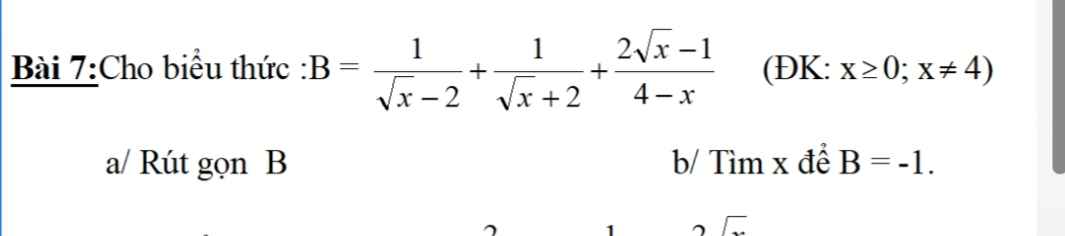1: Gọi phương trình đường thẳng AB là y=ax+b(a\(\ne\)0)
Thay x=1 và y=1 vào y=ax+b, ta được:
\(a\cdot1+b=1\)
=>a+b=1
=>b=1-a
Thay x=2 và y=-1 vào y=ax+b, ta được:
\(a\cdot2+b=-1\)
=>2a+b=-1
=>2a+1-a=-1
=>a+1=-1
=>a=-2(nhận)
\(b=1-\left(-2\right)=1+2=3\)
Vậy: Phương trình đường thẳng AB là y=-2x+3
2: Đặt (d): \(y=\left(m^2-3m\right)x+m^2-2m+2\)
Thay x=0 và y=2 vào (d), ta được:
\(0\left(m^2-3m\right)+m^2-2m+2=2\)
=>\(m^2-2m=0\)
=>m(m-2)=0
=>\(\left[{}\begin{matrix}m=0\\m=2\end{matrix}\right.\)(1)
Vì (d)//AB nên \(\left\{{}\begin{matrix}m^2-3m=-2\\m^2-2m+2\ne3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m^2-3m+2=0\\m^2-2m-1\ne0\end{matrix}\right.\Leftrightarrow m\in\left\{2;1\right\}\left(2\right)\)
Từ (1),(2) suy ra m=2