1: Thay x=2 và y=5 vào y=(2m-1)x+m-3, ta được:
\(2\left(2m-1\right)+m-3=5\)
=>4m-2+m-3=5
=>5m=10
=>m=2
2: y=(2m-1)x+m-3
=2mx-x+m-3
=m(2x+1)-x-3
Tọa độ điểm cố định mà đường thẳng y=(2m-1)x+m-3 luôn đi qua là:
\(\left\{{}\begin{matrix}2x+1=0\\y=-x-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=-1\\y=-x-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=\dfrac{1}{2}-3=-\dfrac{5}{2}\end{matrix}\right.\)
3: Thay \(x=\sqrt{2}-1;y=0\) vào y=(2m-1)x+m-3, ta được:
\(\left(2m-1\right)\cdot\left(\sqrt{2}-1\right)+m-3=0\)
=>\(m\left(2\sqrt{2}-2\right)-\sqrt{2}+1+m-3=0\)
=>\(m\left(2\sqrt{2}-2+1\right)-\sqrt{2}-2=0\)
=>\(m\left(2\sqrt{2}-1\right)=2+\sqrt{2}\)
=>\(m=\dfrac{2+\sqrt{2}}{2\sqrt{2}-1}=\dfrac{6+5\sqrt{2}}{7}\)
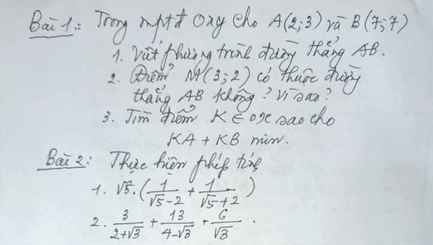làm hộ mik bài 1 thôi nha
