c: \(P=\left(\dfrac{\sqrt{3}\left(\sqrt{3}+\sqrt{2}\right)}{2\left(\sqrt{3}+\sqrt{2}\right)}+\dfrac{\sqrt{3}}{2}\right)\cdot\dfrac{1}{\sqrt{3}}=\sqrt{3}\cdot\dfrac{1}{\sqrt{3}}=1\)
d: \(P=\dfrac{\sqrt{5}\left(\sqrt{5}+1\right)}{\sqrt{5}+1}+\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}+\dfrac{\sqrt{20}\left(\sqrt{3}+\sqrt{5}\right)}{\sqrt{3}+\sqrt{5}}\)
\(=\sqrt{5}+\sqrt{5}+2\sqrt{5}=4\sqrt{5}\)
\(a+b=\sqrt{28+6\sqrt{3}}-\sqrt{31-12\sqrt{3}}=\sqrt{\left(3\sqrt{3}\right)^2+2.3\sqrt{3}+1}-\sqrt{\left(3\sqrt{3}\right)^2-2.2.3\sqrt{3}+2^2}=\sqrt{\left(3\sqrt{3}+1\right)^2}-\sqrt{\left(3\sqrt{3}-2\right)^2}=3\sqrt{3}+1-3\sqrt{3}+2=3\)
\(\Rightarrow P=\left(a+b\right)^2-2ab+4\left(a+b\right)+2ab=\left(a+b\right)^2+4\left(a+b\right)=3^2+4.3=21\)
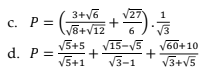
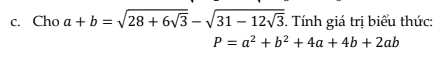
Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.
