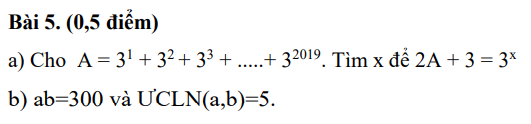Question

mn ơi làm hộ mình 2 bài này với,ai làm nhanh nhất mình tim cho ! 

Answer 1

Bài 6 :
a) 7n + 10 và 5n + 7 
ƯCLN( 7n + 10 ; 5n + 7 ) = d
=> 7n + 10 chia hết d
5n + 7 chia hết d
5.(7n + 10) = 35n + 50 chia hết d
7.(5n + 7 ) = 35n + 49 chia hết d
=> ( 35n + 50 ) - ( 35n + 49 ) chia hết d
35n + 50 - 35n - 49 chia hết d
( 35n - 35n ) + ( 50 - 49 ) chia hết d 
0 + 1 chia hết d
=> 1 chia hết d 
suy ra d = 1 
Vậy ƯCLN ( 7n + 10 ; 5n + 7 ) = 1
b) làm tương tự câu a 
Bài 7 : 
a) Chứng minh chia hết 4 
A = 3¹ + 3² + 3³ +... + 3¹¹⁹ + 3¹²⁰
A = ( 3¹ + 3² ) + (3³ + 3⁴ ) + ... + ( 3¹¹⁹ + 3¹²⁰ )
A = 3¹ . ( 1 + 3 ) + 3³ . ( 1 + 3 ) + ... + 3¹¹⁹. ( 1 + 3 )
A = 3¹ . 4 + 3³ . 4 + ... + 3¹¹⁹ . 4 
A = 4. ( 3¹ + 3³ + ... + 3¹¹⁹ ) chia hết 4
Chia hết cho 13 thì làm tương tự  
Câu b mik chx bt làm ^.^

Answer 2

\(b,A=3^1+3^2+...+3^{120}\)

\(\Rightarrow3A=3^2+3^3+...+3^{121}\)

\(\Rightarrow3A-A=3^2+3^3+...+3^{121}-3-3^2-...-3^{120}\)

\(\Rightarrow2A=3^{121}-3\)

Ta có:\(2A-3=3^{121}-3-3=3^{121}-6\) 

⇒đề sai phải lá 2A+3