Bài 19:
Trên tia đối của tia HB lấy điểm D sao cho HD = HC.
\(\Rightarrow\Delta ACD\) cân tại \(A\) nên \(\widehat{CAH}=\widehat{DAH}\)
Và \(\widehat{ACB}=\widehat{CAH}+\widehat{AHC}\left(góc.ngoài.\Delta ACH\right)\)
\(\Rightarrow\widehat{ACB}-\widehat{CAH}=\widehat{AHC}=90^o\left(1\right)\)
Mặt khác: \(\widehat{ACB}-\widehat{ABC}=90^o\left(gt\right)\left(2\right)\)
Từ (1) và (2) suy ra:
\(\widehat{CAH}=\widehat{ABC}=\widehat{DAH}\)
\(\Rightarrow\widehat{B}+\widehat{D}=90^o\)
Do đó: tg ABC là tg vuông và vuông tại A.
Trong tg ABD có \(\widehat{BAD}=90^o;AH\perp BD\) nên \(AH^2=HB.HD\)
\(\Rightarrow AH^2=HB.HC\left(vì.HD=HC\right)\)
, mình đang cần giải gấp. Cảm ơn mn nhiều.
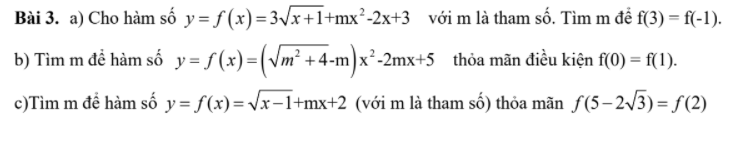
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
