ĐKXĐ:\(x\ne\pm3\)
\(\dfrac{1}{x+3}-\dfrac{2x-1}{x-3}=\dfrac{x^2-15}{x^2-9}\\ \Leftrightarrow\dfrac{x-3}{\left(x+3\right)\left(x-3\right)}-\dfrac{\left(x+3\right)\left(2x-1\right)}{\left(x+3\right)\left(x-3\right)}-\dfrac{x^2-15}{\left(x+3\right)\left(x-3\right)}=0\\ \Leftrightarrow\dfrac{x-3-\left(2x^2+6x-x-3\right)-\left(x^2-15\right)}{\left(x+3\right)\left(x-3\right)}=0\\ \Rightarrow x-3-2x^2-6x+x+3-x^2+15=0\\ \Leftrightarrow-3x^2-4x+15=0\\ \Leftrightarrow3x^2+4x-15=0\\ \Leftrightarrow\left(3x^2+9x\right)-\left(5x+15\right)=0\\ \Leftrightarrow3x\left(x+3\right)-5\left(x+3\right)=0\\ \Leftrightarrow\left(x+3\right)\left(3x-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\left(ktm\right)\\x=\dfrac{5}{3}\left(tm\right)\end{matrix}\right.\)
\(PT\left(x\ne3;-3\right).\\ \Leftrightarrow\dfrac{x-3-\left(2x-1\right)\left(x+3\right)-x^2+15}{\left(x+3\right)\left(x-3\right)}=0.\\ \Rightarrow x-3-2x^2-5x+3-x^2+15=0.\\ \Leftrightarrow-3x^2-4x+15=0.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{3}\left(TM\right).\\x=-3\left(koTM\right).\end{matrix}\right.\)
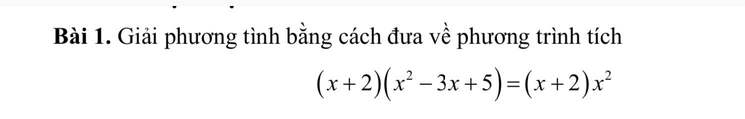
vẽ hình giúp mik nha mik cảm ơn rất rất nhiều
lm giúp mik vs mn mik cần gấp
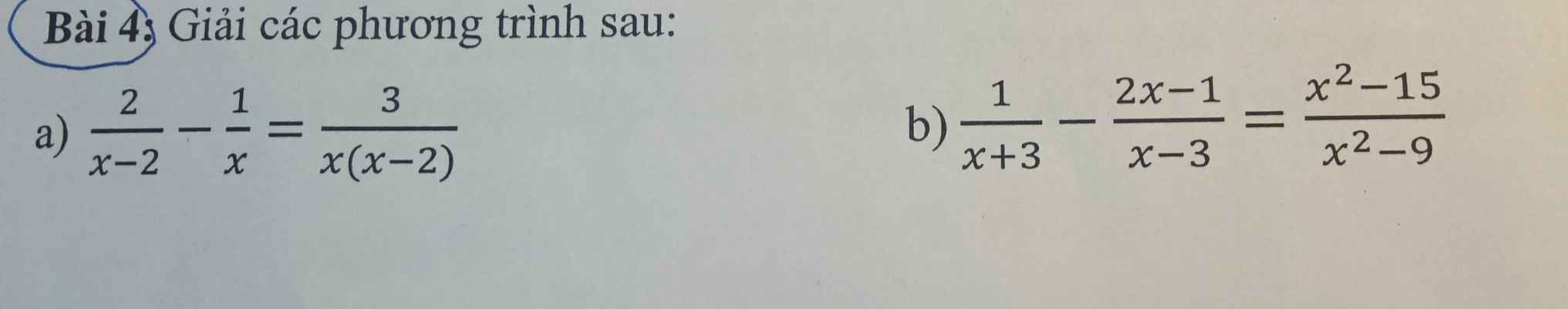
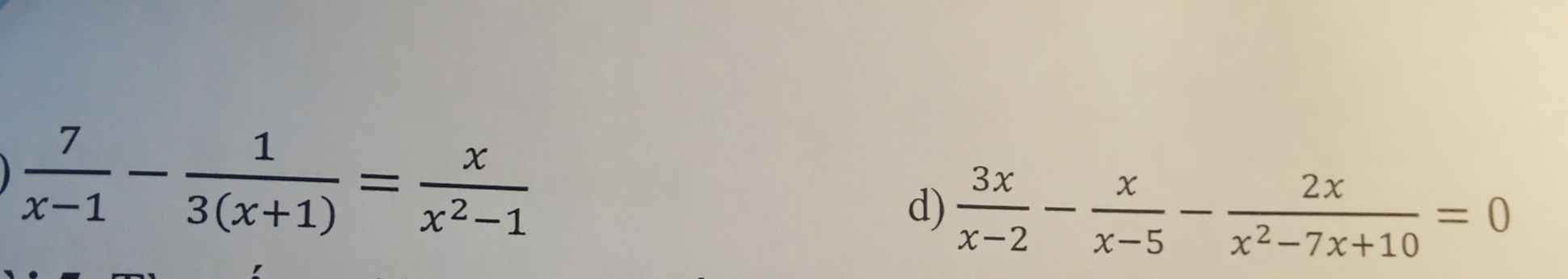Mn giúp mik vs