ĐKXĐ: a>0; b>0
\(\dfrac{\sqrt{a}+1}{\sqrt{ab}+1}+\dfrac{\sqrt{ab}+\sqrt{a}}{\sqrt{ab}-1}-1\)
\(=\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{ab}-1\right)+\left(\sqrt{ab}+\sqrt{a}\right)\left(\sqrt{ab}+1\right)-\left(ab-1\right)}{ab-1}\)
\(=\dfrac{a\sqrt{b}-\sqrt{a}+\sqrt{ab}-1+ab+\sqrt{ab}+a\sqrt{b}+\sqrt{a}-ab+1}{ab-1}\)
\(=\dfrac{2a\sqrt{b}+2\sqrt{ab}}{ab-1}=\dfrac{2\sqrt{ab}\left(\sqrt{a}+1\right)}{ab-1}\)
\(\dfrac{\sqrt{a}+1}{\sqrt{ab}+1}-\dfrac{\sqrt{ab}+\sqrt{a}}{\sqrt{ab}-1}+1\)
\(=\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{ab}-1\right)-\left(\sqrt{ab}+\sqrt{a}\right)\left(\sqrt{ab}+1\right)+ab-1}{ab-1}\)
\(=\dfrac{a\sqrt{b}-\sqrt{a}+\sqrt{ab}-1-ab-\sqrt{ab}-a\sqrt{b}-\sqrt{a}+ab-1}{ab-1}\)
\(=\dfrac{-2\sqrt{a}-2}{ab-1}=\dfrac{-2\left(\sqrt{a}+1\right)}{ab-1}\)
\(P=\left(\dfrac{\sqrt{a}+1}{\sqrt{ab}+1}+\dfrac{\sqrt{ab}+\sqrt{a}}{\sqrt{ab}-1}-1\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{ab}+1}-\dfrac{\sqrt{ab}+\sqrt{a}}{\sqrt{ab}-1}+1\right)\)
\(=\dfrac{2\sqrt{ab}\left(\sqrt{a}+1\right)}{ab-1}:\dfrac{-2\left(\sqrt{a}+1\right)}{ab-1}\)
\(=-\dfrac{2\sqrt{ab}\left(\sqrt{a}+1\right)}{ab-1}\cdot\dfrac{ab-1}{2\left(\sqrt{a}+1\right)}=\sqrt{ab}\)
ĐKXĐ: x>0; x<>1
\(A=\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{1}{\sqrt{x}+1}\right)\cdot\left(1-\dfrac{1}{\sqrt{x}}\right)\)
\(=\dfrac{\sqrt{x}+1+\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}-1}{\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}}{\sqrt{x}+1}\cdot\dfrac{1}{\sqrt{x}}=\dfrac{2}{\sqrt{x}+1}\)
ĐKXĐ: x>0; x<>1
\(B=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\right)\cdot\left(1+\dfrac{1}{\sqrt{x}}\right)\)
\(=\dfrac{\left(\sqrt{x}+1\right)^2-\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
\(=\dfrac{x+2\sqrt{x}+1-x+2\sqrt{x}-1}{\left(\sqrt{x}-1\right)\cdot\sqrt{x}}=\dfrac{4\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}=\dfrac{4}{\sqrt{x}-1}\)
ĐKXĐ: a>=0; a<>4
\(C=\dfrac{\sqrt{a}+3}{\sqrt{a}-2}-\dfrac{\sqrt{a}-1}{\sqrt{a}+2}+\dfrac{4\sqrt{a}-4}{4-a}\)
\(=\dfrac{\left(\sqrt{a}+3\right)\left(\sqrt{a}+2\right)-\left(\sqrt{a}-1\right)\left(\sqrt{a}-2\right)-\left(4\sqrt{a}-4\right)}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}\)
\(=\dfrac{a+5\sqrt{a}+6-\left(a-3\sqrt{a}+2\right)-4\sqrt{a}+4}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}\)
\(=\dfrac{a+\sqrt{a}+10-a+3\sqrt{a}-2}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}=\dfrac{4\left(\sqrt{a}+2\right)}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}\)
\(=\dfrac{4}{\sqrt{a}-2}\)
ĐKXĐ: x>0; x<>1
\(D=\left(\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}-\dfrac{\sqrt{x}-2}{x-1}\right)\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
\(=\left(\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2}-\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
\(=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)^2\cdot\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}+1}{\sqrt[]{x}}\)
\(=\dfrac{x+\sqrt{x}-2-\left(x-\sqrt{x}-2\right)}{x-1}\cdot\dfrac{1}{\sqrt{x}}=\dfrac{2\sqrt{x}}{\sqrt{x}\left(x-1\right)}=\dfrac{2}{x-1}\)
Mn giúp mik với,bh mik đang cần gấp lắm 19h30 mik phải có bài r nên mn giúp mik với 
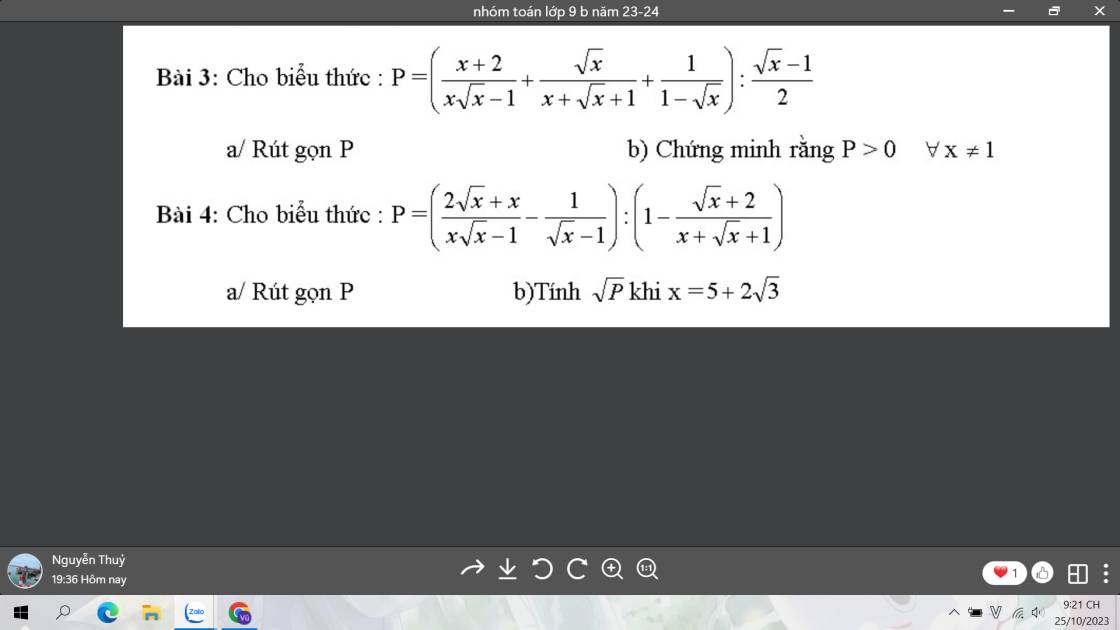giải giúp mik bài 3 nha mn <3
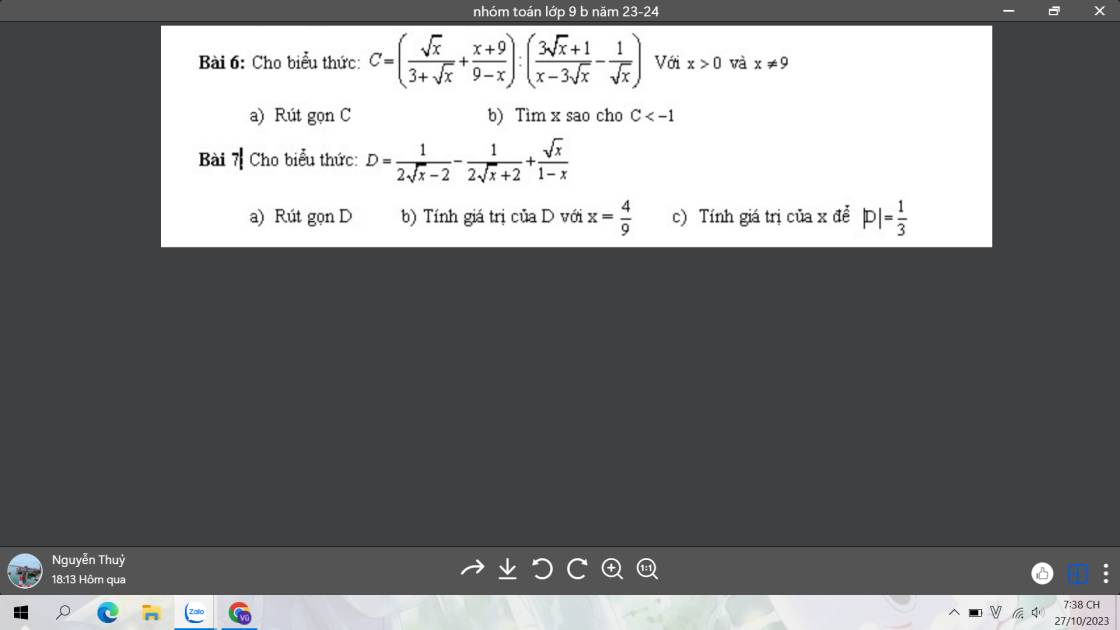giúp mik với mn ơi mik đg cần gấp