Đặt \(A=2x^2+x\)
⇒\(2A=4x^2+2x\)
\(=\left[\left(2x\right)^2+2x+1\right]-1\)
\(=\left(2x+1\right)^2-1\)
\(=-1+\left(2x+1\right)^2\)
⇒\(A=\dfrac{-1+\left(2x+1\right)^2}{2}\)
\(=-\dfrac{1}{2}+\dfrac{\left(2x+1\right)^2}{2}\)
Vì \(\dfrac{\left(2x+1\right)^2}{2}\text{≥}0\)
⇒ \(A\text{≥}-\dfrac{1}{2}\)
Min \(A=-\dfrac{1}{2}\) ⇔ \(\dfrac{\left(2x+1\right)^2}{2}=0\)
⇔\(2x+1=0\)
⇔\(x=-\dfrac{1}{2}\)










 Mn giúp em bài 3 câu bc với em tính số xấu quá, mong mn giúp ạ:(
Mn giúp em bài 3 câu bc với em tính số xấu quá, mong mn giúp ạ:(


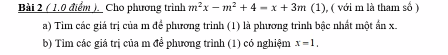 Mn giúp em với ạ, em cần gấp
Mn giúp em với ạ, em cần gấp Mn giúp em với ạ:(
Mn giúp em với ạ:(
 mn giúp em với ạ!
mn giúp em với ạ!