7. Ta có: \(\left(x+\sqrt{x^2+3}\right)\left(\sqrt{x^2+3}-x\right)=x^2+3-x=3\)
\(\Rightarrow\sqrt{x^2+3}-x=y+\sqrt{y^2+3}\Rightarrow x+y=\sqrt{x^2+3}-\sqrt{y^2+3}\left(1\right)\)
Lại có \(\left(y+\sqrt{y^2+3}\right)\left(\sqrt{y^2+3}-y\right)=y^2+3-y=3\)
\(\Rightarrow\sqrt{x^2+3}+x=\sqrt{y^2+3}-y\Rightarrow x+y=\sqrt{y^2+3}-\sqrt{x^2+3}\left(2\right)\)
Lấy \(\left(1\right)+\left(2\right)\Rightarrow2\left(x+y\right)=0\Rightarrow x+y=0\)
9. Ta có: \(\sqrt{55+\sqrt{109}}-\sqrt{55-\sqrt{109}}\)
\(=\sqrt{\dfrac{110+2\sqrt{109}}{2}}-\sqrt{\dfrac{110-2\sqrt{109}}{2}}\)
\(=\sqrt{\dfrac{\left(\sqrt{109}+1\right)^2}{2}}-\sqrt{\dfrac{\left(\sqrt{109}-1\right)^2}{2}}=\dfrac{\sqrt{109}+1}{\sqrt{2}}-\dfrac{\sqrt{109}-1}{\sqrt{2}}\)
\(=\dfrac{2}{\sqrt{2}}=\sqrt{2}\)
Lại có: \(\dfrac{\sqrt{2-\sqrt{4y-y^2}}}{y-2}.\sqrt{4+2\sqrt{4y-y^2}}\)
\(=\dfrac{\sqrt{4-2\sqrt{y\left(4-y\right)}}}{\sqrt{2}\left(y-2\right)}.\sqrt{\left(\sqrt{y}\right)^2+2\sqrt{y\left(4-y\right)}+\left(\sqrt{4-y}\right)^2}\)
\(\dfrac{\sqrt{\left(\sqrt{y}\right)^2-2\sqrt{y\left(4-y\right)}+\left(\sqrt{4-y}\right)^2}}{\sqrt{2}\left(y-2\right)}.\sqrt{\left(\sqrt{y}+\sqrt{4-y}\right)^2}\)
\(=\dfrac{\sqrt{\left(\sqrt{y}-\sqrt{4-y}\right)^2}}{\sqrt{2}\left(y-2\right)}.\left|\sqrt{y}+\sqrt{4-y}\right|=\dfrac{\left|\sqrt{y}-\sqrt{4-y}\right|}{\sqrt{2}\left(y-2\right)}.\left|\sqrt{y}+\sqrt{4-y}\right|\)
Vì \(y>2\Rightarrow\left\{{}\begin{matrix}\sqrt{y}>\sqrt{2}\\\sqrt{4-y}< \sqrt{2}\end{matrix}\right.\Rightarrow\sqrt{y}-\sqrt{4-y}>0\)
\(\Rightarrow\dfrac{\left|\sqrt{y}-\sqrt{4-y}\right|}{\sqrt{2}\left(y-2\right)}.\left|\sqrt{y}+\sqrt{4-y}\right|=\dfrac{\left(\sqrt{y}-\sqrt{4-y}\right)\left(\sqrt{y}+\sqrt{4+y}\right)}{\sqrt{2}\left(y-2\right)}\)
\(=\dfrac{y-\left(4-y\right)}{\sqrt{2}\left(y-2\right)}=\dfrac{2y-4}{\sqrt{2}\left(y-2\right)}=\dfrac{2\left(y-2\right)}{\sqrt{2}\left(y-2\right)}=\sqrt{2}\)
\(\Rightarrow\dfrac{\sqrt{2-\sqrt{4y-y^2}}}{y-2}.\sqrt{4+2\sqrt{4y-y^2}}=\sqrt{55+\sqrt{109}}-\sqrt{55-\sqrt{109}}\)
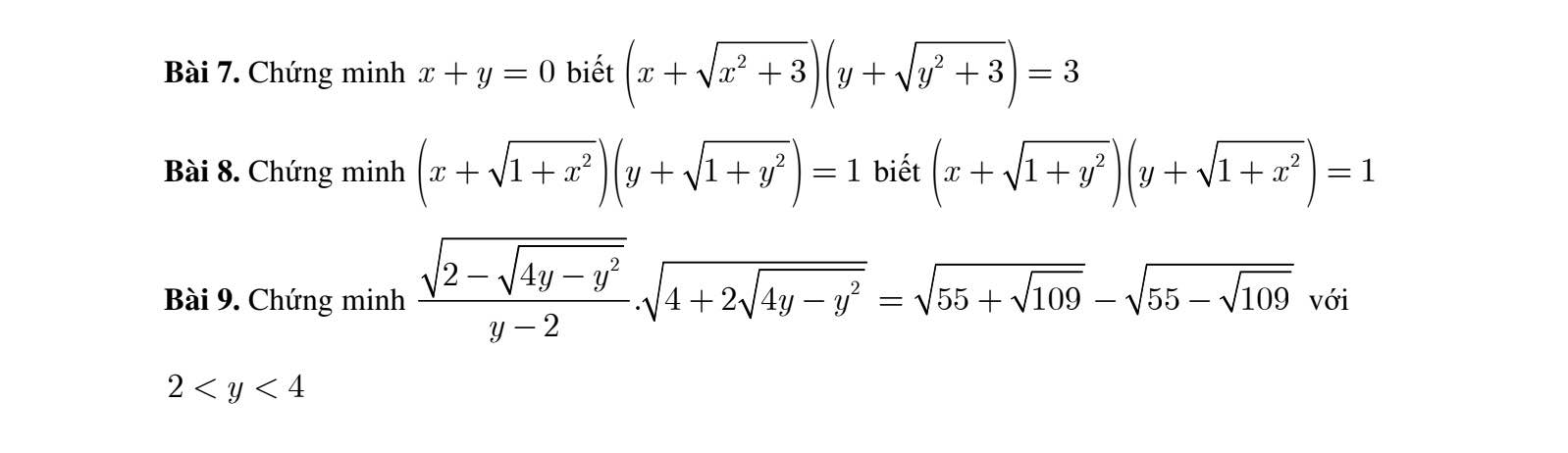
được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều. 