Bài 7:
\(A=\frac{2019^{100}+2019^{96}+2019^{92}+...+2019^4+1}{2019^{102}+2019^{100}+...+2019^2+1}\)
Gọi tử số là $M$ và mẫu số là $N$
Xét tử số:
\(M=2019^{100}+2019^{96}+...+2019^4+1\)
\(2019^{4}M=2019^{104}+2019^{100}+...+2019^8+2019^4\)
\(M(2019^4-1)=2019^{104}-1\)
Xét mẫu số:
\(N=2019^{102}+2019^{100}+...+2019^2+1\)
\(2019^2.N=2019^{104}+2019^{102}+...+2019^4+2019^2\)
\(N(2019^2-1)=2019^{104}-1\)
Do đó:
\(A=\frac{\frac{2019^{104}-1}{2019^4-1}}{\frac{2019^{104}-1}{2019^2-1}}=\frac{2019^2-1}{2019^4-1}=\frac{1}{2019^2+1}\)
\(4A=\frac{4}{2019^2+1}=\frac{4}{4076362}< \frac{4}{4000000}=\frac{1}{1000000}=(0,1)^6\)
Bài 8:
Ta có:
\(95^8<100^8=(10^2)^8=10^{16}\)
\(\frac{95^8}{100^8}>\frac{90^8}{100^8}=(\frac{9}{10})^8> \frac{9}{10}.\frac{8}{9}.\frac{7}{8}....\frac{2}{3}=\frac{2}{10}>\frac{1}{10}\)
\(\Rightarrow 95^8> \frac{100^8}{10}=10^{15}\)
Vậy \(10^{16}> 95^8> 10^{15}\Rightarrow 95^8\) có 16 chữ số







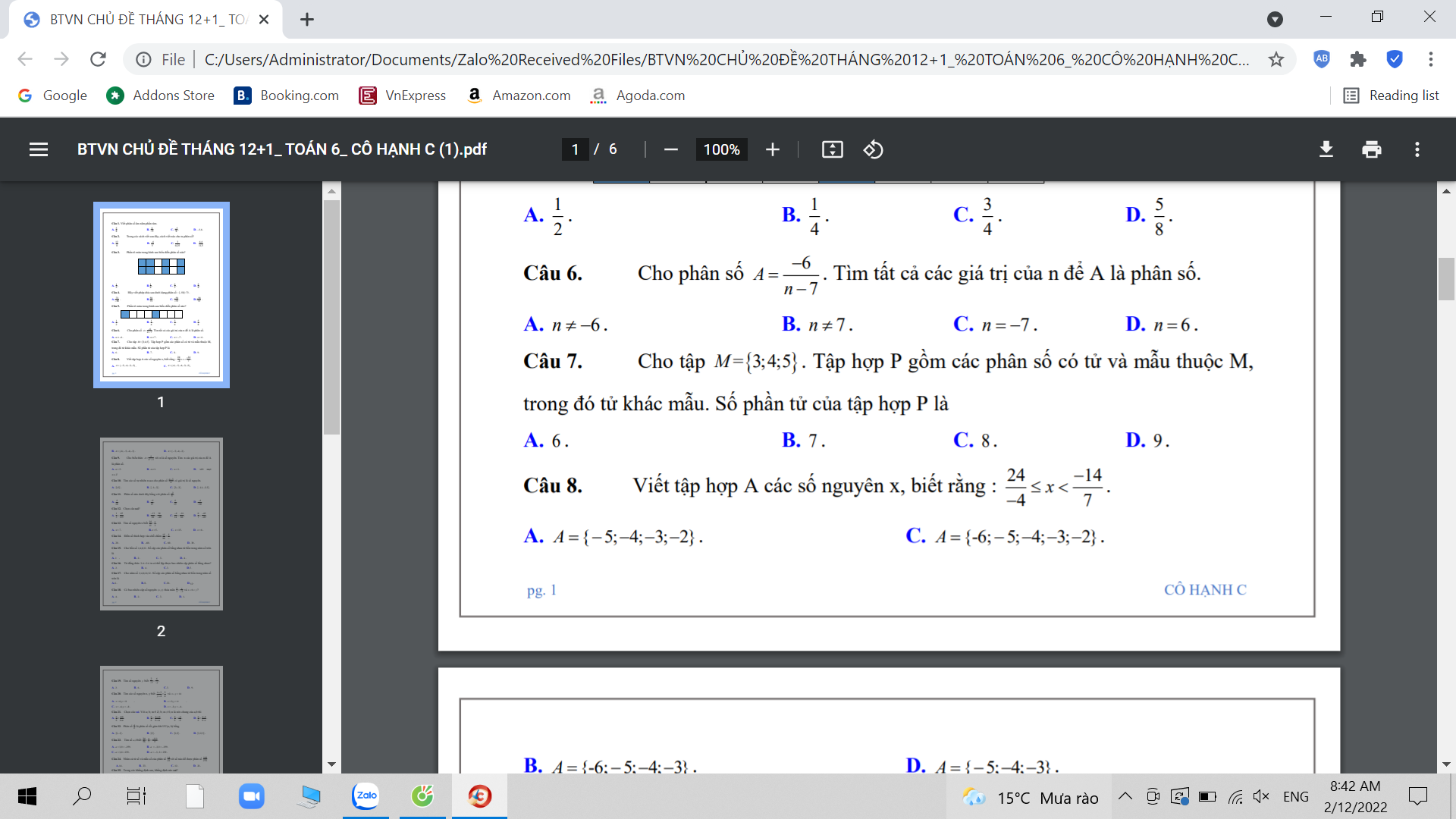 mọi người giúp em với ạ em đang cần gấp!!
mọi người giúp em với ạ em đang cần gấp!!