xét tam gúac AFD có AE = EF ; AD = DG
=> ED là đường trung bình of tam giác AFD
=> ED = 1/2 FG
=>ED = 6 => x = 6 cm
xét hình thang EDCB ( ED // BC ) có :
EF = FB ; DG = GC
=> GF là đường trung bình of hình thanh EDCB
=> FG = ( ED + BC ) : 2
=> 24 = 6 + BC
=> BC = 18 cm
xét tam giác afg có
e là t/đ af (ea=ef)
d là t/đ ag(da=dg)
Suy ra de là đường trung bình tam giác agf
=> \(de=\dfrac{fg}{2}\left(dl\right)=>de=\dfrac{12}{2}=>de=6\left(cm\right)\)
xét tứ giác edcb có
ed//cb (gt)
Suy ra edcb là hình thang
xét hình thang edcb có
f là t/đ ed (ef=bf)
g là t/đ dc (gd=gc)
Suy ra fg là đường trung bình hình thang edcb
\(=>fg=\dfrac{ed+bc}{2}\left(dl\right)=>bc=fg\cdot2-ed=>bc=12\cdot2-6=18\left(cm\right)\)

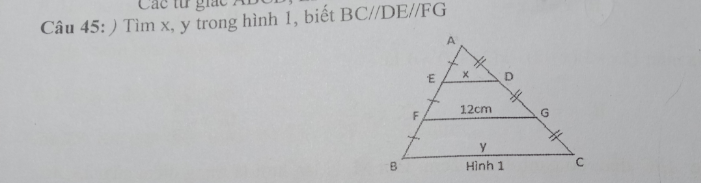








 mn giải giúp em vơi ạ em đang cần gấp cảm ơn
mn giải giúp em vơi ạ em đang cần gấp cảm ơn

 Mn giải giúp mik vs ạ 🥺 mình đang cần gấp. Cảm ơn mn nhiều
Mn giải giúp mik vs ạ 🥺 mình đang cần gấp. Cảm ơn mn nhiều



 ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn