mn cho em xin hình bài này gấp ạ
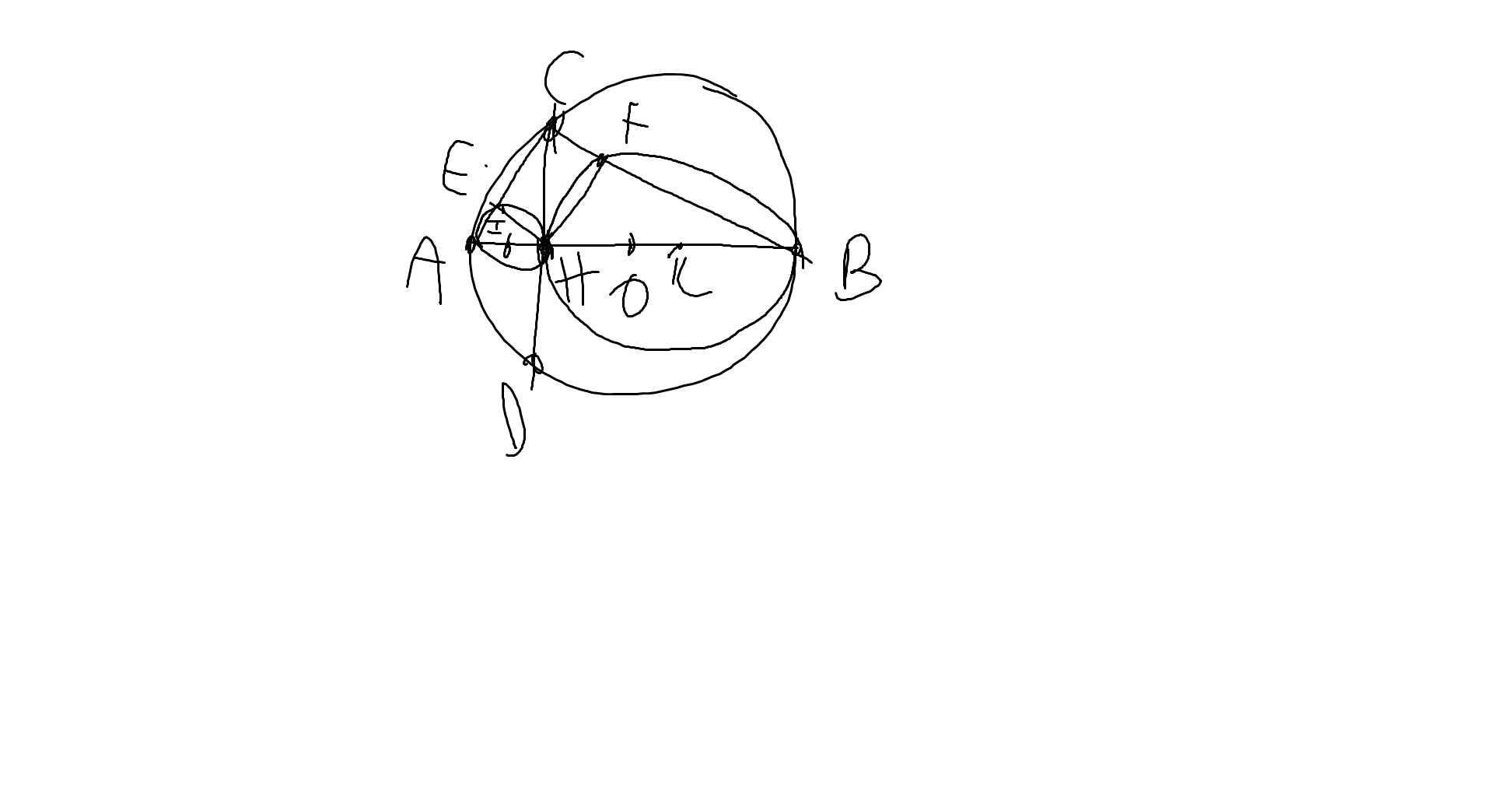
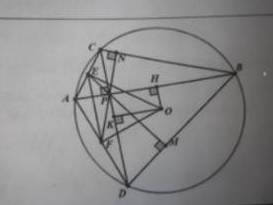
Bài 13. Cho đường tròn (O) có đường kính AB, dây cung CD vuông góc với AB tại H. Gọi E, F theo thứ tự là chân các đường vuông góc kẻ từ H đến CA, CB.
a) Tứ giác CEHF là hình gì? Vì sao?
b) Gọi (I), (K) theo thứ tự là đường tròn đường kính AH và BH. Hãy xác định vị trí tương đối của các cặp đường tròn: (I) và (O); (I) và (K). Tính bán kính của các đường tròn (I) và (K), nếu biết \(AB = 12 \, \text{cm}\) và \(CD = 8 \, \text{cm}\).
a: Xét (O) có
ΔCAB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
Xét tứ giác CEHF có \(\widehat{CEH}=\widehat{CFH}=\widehat{ECF}=90^0\)
nên CEHF là hình chữ nhật
b:
I là tâm đường tròn đường kính AH nên I là trung điểm của AH
=>IA=IH
Ta có: OI+IA=OA
=>OI=OA-IA=R-r
=>(O) và (I) tiếp xúc trong với nhau nhau tại A
Vì HI+HK=IK
nên (I) và (K) tiếp xúc ngoài với nhau nhau tại H