Mình đang cần gấp có thể giúp mình được không? Có thể giải thích chi tiết cho mình bất đẳng thức cauchy nếu được áp dụng trong bài được không?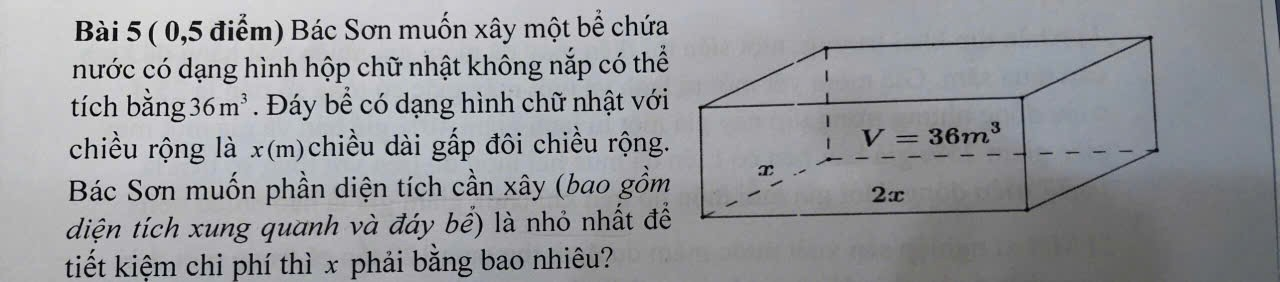
Bài 5 (0,5 điểm) Bác Sơn muốn xây một bể chứa nước có dạng hình hộp chữ nhật không nắp có thể tích bằng \(36m^3\). Đáy bể có dạng hình chữ nhật với chiều rộng là \(x\) (m) chiều dài gấp đôi chiều rộng. Bác Sơn muốn phần diện tích cần xây (bao gồm diện tích xung quanh và đáy bể) là nhỏ nhất để tiết kiệm chi phí thì \(x\) phải bằng bao nhiêu?
Để giải quyết bài toán này, ta cần tìm giá trị của \(x\) để diện tích cần xây là nhỏ nhất.
**Bất đẳng thức Cauchy-Schwarz** có thể được sử dụng để tìm giá trị tối ưu trong một số bài toán tối ưu hóa. Tuy nhiên, trong bài toán này, ta có thể sử dụng phương pháp khác như đạo hàm để tìm giá trị tối ưu.
### Giải thích chi tiết:
1. **Thiết lập bài toán:**
- Thể tích của bể: \( V = x \cdot 2x \cdot h = 36 \).
- Diện tích cần xây (diện tích xung quanh và đáy):
\[
A = 2(xh + 2xh) + x \cdot 2x = 6xh + 2x^2
\]
2. **Tìm \( h \) từ thể tích:**
\[
x \cdot 2x \cdot h = 36 \implies 2x^2h = 36 \implies h = \frac{18}{x^2}
\]
3. **Thay \( h \) vào biểu thức diện tích:**
\[
A = 6x \left(\frac{18}{x^2}\right) + 2x^2 = \frac{108}{x} + 2x^2
\]
4. **Tối ưu hóa diện tích:**
- Tính đạo hàm của \( A \) theo \( x \):
\[
A' = -\frac{108}{x^2} + 4x
\]
- Giải phương trình \( A' = 0 \):
\[
-\frac{108
Gọi \(h>0\left(m\right):\) là chiều cao của bể
Thể tích bể : \(V=2x.x.h=2x^2h=36\left(m^3\right)\Rightarrow h=\dfrac{18}{x^2}\)
Diện tích đáy: \(S_{đáy}=2x.x=2x^2\left(m^2\right)\)
Diện tích xung quanh : \(S_{xq}=2\left(2x+x\right)h=6xh\left(m^2\right)\)
Diện tích toàn phần: \(S_{tp}=S_{đáy}+S_{xq}=2x^2+6xh=2x^2+6x.\dfrac{18}{x^2}=2x^2+\dfrac{108}{x}\)
\(S_{tp}=2x^2-12x+18+\dfrac{108}{x}+12x-18=2\left(x-3\right)^2+\dfrac{108}{x}+12x-18\)
mà \(\dfrac{108}{x}+12x\ge2\sqrt{\dfrac{108}{x}.12x}=72\left(Bđt.Cauchy\right)\), Dấu '=' xảy ra khi \(x=3\)
\(\Rightarrow S_{tp}\ge0+72-18=54\left(m^2\right)\)
Dùng đạo hàm HS \(f\left(x\right)=2x^2+\dfrac{108}{x}\) cũng đạt cực tiểu tại \(x=3\) và \(f\left(x\right)_{min}=f\left(x=3\right)=2.3^2+\dfrac{108}{3}=18+36=54\left(m^2\right)\)
\(\Rightarrow\) Cả hai phương pháp cùng ra 1 đáp án
\(\Rightarrow\) Để diện tích toàn phần của bể nhỏ nhất thì chiều rộng của đáy bể là \(x=3\left(m\right)\)
Vậy, bác Sơn nên xây bể nước có chiều rộng đáy là \(3\left(m\right)\) để tiết kiệm chi phí nhất.





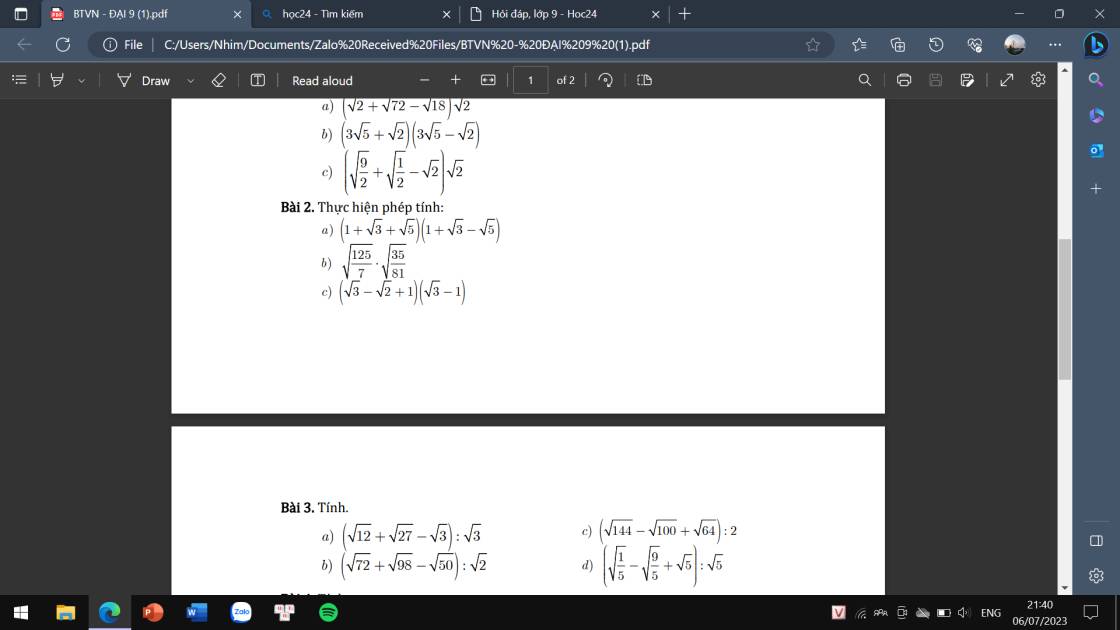






 Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn




