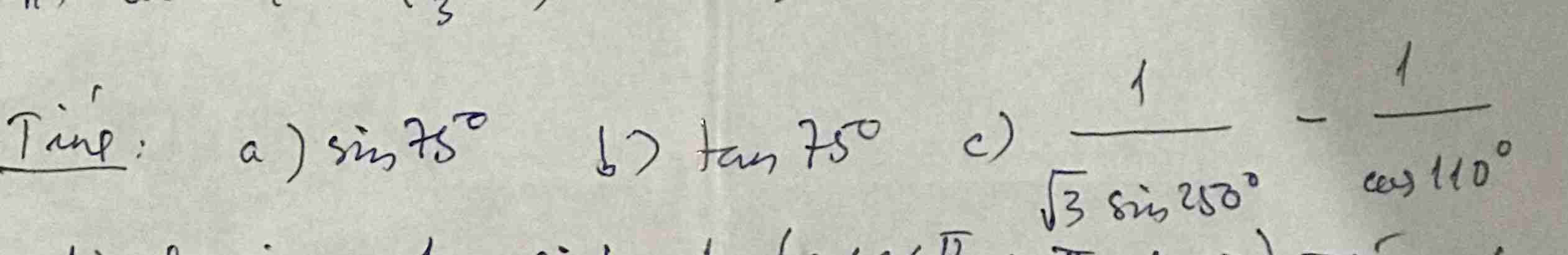a: \(sin75^0=sin\left(30^0+45^0\right)\)
\(=sin30^0\cdot cos45^0+cos30^0\cdot sin45^0\)
\(=\dfrac{1}{2}\cdot\dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{2}}{2}\)
\(=\dfrac{\sqrt{2}+\sqrt{6}}{4}\)
b: \(tan75=tan\left(30+45\right)\)
\(=\dfrac{tan30+tan45}{1-tan30\cdot tan45}\)
\(=\dfrac{\dfrac{\sqrt{3}}{3}+1}{1-\dfrac{\sqrt{3}}{3}\cdot1}=\dfrac{3+\sqrt{3}}{3}:\dfrac{3-\sqrt{3}}{3}=\dfrac{3+\sqrt{3}}{3-\sqrt{3}}\)
\(=\dfrac{\left(3+\sqrt{3}\right)^2}{\left(3+\sqrt{3}\right)\left(3-\sqrt{3}\right)}=\dfrac{12+6\sqrt{3}}{9-3}=2+\sqrt{3}\)
c: \(\dfrac{1}{\sqrt{3}\cdot sin250^0}-\dfrac{1}{cos110^0}\)
\(=\dfrac{1}{\sqrt{3}\cdot sin\left(360^0-110^0\right)}-\dfrac{1}{cos110^0}\)
\(=\dfrac{1}{\sqrt{3}\cdot sin\left(-110^0\right)}-\dfrac{1}{cos110^0}=\dfrac{-1}{\sqrt{3}\cdot sin110^0}-\dfrac{1}{cos110^0}\)
\(=\dfrac{-cos110^0-\sqrt{3}\cdot sin110^0}{\sqrt{3}\cdot sin110^0\cdot cos110^0}=\dfrac{-\dfrac{1}{2}\cdot cos110^0-\dfrac{\sqrt{3}}{2}\cdot sin110^0}{\dfrac{\sqrt{3}}{2}\cdot\dfrac{1}{2}\cdot2\cdot sin110^0\cdot cos110^0}\)
\(=-\dfrac{cos110^0\cdot sin30^0+sin110^0\cdot cos30^0}{\dfrac{\sqrt{3}}{2}\cdot sin220^0}\)
\(=-\dfrac{sin140^0}{\dfrac{\sqrt{3}}{2}\cdot sin220^0}\)