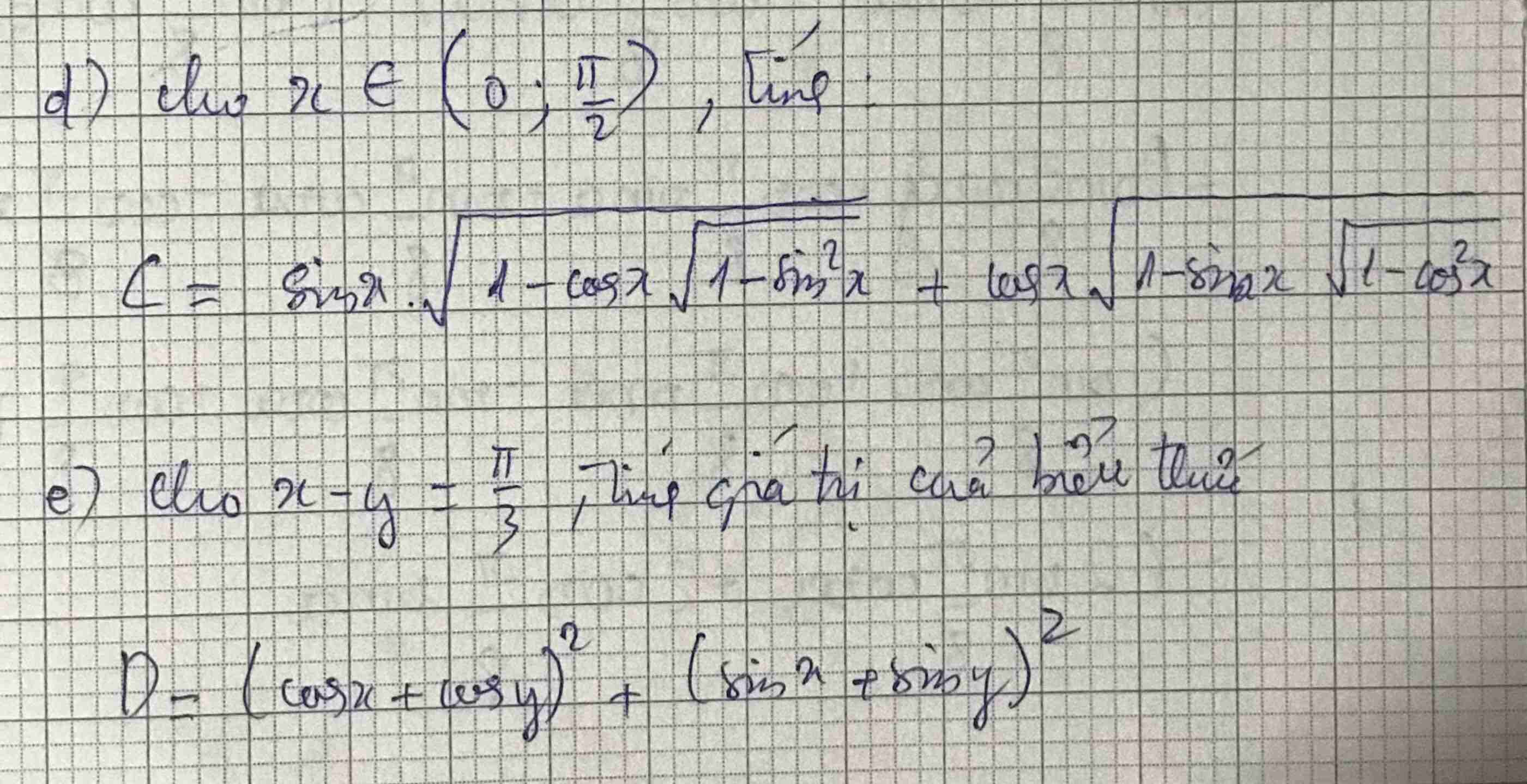e: \(D=\left(cosx+cosy\right)^2+\left(sinx+siny\right)^2\)
\(=cos^2x+cos^2y+2\cdot cosx\cdot cosy+sin^2x+sin^2y+2\cdot siny\cdot sinx\)
\(=1+1+2\cdot\left(cosx\cdot cosy+sinx\cdot siny\right)\)
\(=2+2\cdot cos\left(x-y\right)=2+2\cdot cos\left(\dfrac{\Omega}{3}\right)=3\)
d: \(C=sinx\cdot\sqrt{1-cosx\cdot\sqrt{1-sin^2x}}+cosx\cdot\sqrt{1-sinx\cdot\sqrt{1-cos^2x}}\)
\(=sinx\cdot\sqrt{1-cosx\cdot cosx}+cosx\cdot\sqrt{1-sinx\cdot sinx}\)
\(=sinx\cdot\sqrt{1-cos^2x}+cosx\cdot\sqrt{1-sin^2x}\)
\(=sin^2x+cos^2x=1\)
Đúng 2
Bình luận (0)
