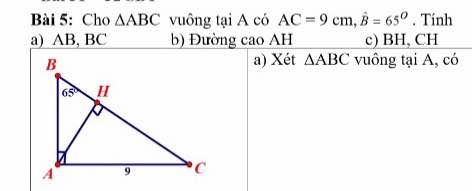
\(a,\tan\widehat{B}=\dfrac{AC}{AB}=\tan65^0\approx2\Leftrightarrow AB=\dfrac{AC}{2}=4,5\left(cm\right)\\ \Leftrightarrow BC=\sqrt{AB^2+AC^2}=\dfrac{9\sqrt{5}}{2}\left(cm\right)\\ b,Áp.dụng.HTL:AH\cdot BC=AB\cdot AC=40,5\Leftrightarrow AH=\dfrac{40,5}{BC}=\dfrac{9\sqrt{5}}{5}\left(cm\right)\)
\(c,Áp.dụng.HTL:\\ \left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=\dfrac{9\sqrt{5}}{10}\left(cm\right)\\CH=\dfrac{AC^2}{BC}=\dfrac{18\sqrt{5}}{5}\left(cm\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)
