Bài 8:
\(B=\frac{a}{ab+a+abc}+\frac{b}{bc+b+1}+\frac{2c}{ac+2c+abc}\\ =\frac{1}{b+1+bc}+\frac{b}{bc+b+1}+\frac{2}{a+2+ab}\\ =\frac{1}{b+1+bc}+\frac{b}{bc+b+1}+\frac{abc}{a+abc+ab}\\ =\frac{1}{b+1+bc}+\frac{b}{bc+b+1}+\frac{bc}{1+bc+b}\\ =\frac{1+b+bc}{b+1+bc}=1\)
Bài 9:
\(A=\frac{a}{ab+a+1}+\frac{ba}{abc+ab+a}+\frac{c.ab}{ac.ab+c.ab+ab}\\ =\frac{a}{ab+a+1}+\frac{ab}{1+ab+a}+\frac{1}{a+1+ab}\\ =\frac{ab+a+1}{ab+a+1}=1\)
Bài 10:
\((x-1)^{20}\geq 0, \forall x; (y+2)^{20}\geq 0, \forall y\)
Do đó để tổng $(x-1)^{20}+(y+2)^{20}=0$ thì $(x-1)^{20}=(y+2)^{20}=0$
$\Rightarrow x=1; y=-2$
Khi đó:
$A=2.1^5-5.(-2)^3+4=46$
Bài 11:
$|x-1|=2$
$\Rightarrow x-1=2$ hoặc $x-1=-2$
$\Rightarrow x=3$ hoặc $x=-1$
Nếu $x=3$ thì:
$A=5.3^2+6.3-2=61$
Nếu $x=-1$ thì:
$A=5(-1)^2+6(-1)-2=-3$
Bài 12:
$(x-\frac{1}{2})^{x+1}-(x-\frac{1}{2})^{x+11}=0$
$\Rightarrow (x-\frac{1}{2})^{x+1}[1-(x-\frac{1}{2})^{10}]=0$
$\Rightarrow (x-\frac{1}{2})^{x+1}=0$ hoặc $1-(x-\frac{1}{2})^{10}=0$
Nếu $(x-\frac{1}{2})^{x+1}=0$
$\Rightarrow x-\frac{1}{2}=0$
$\Rightarrow x=\frac{1}{2}$
Nếu $1-(x-\frac{1}{2})^{10}=0$
$\Rightarrow (x-\frac{1}{2})^{10}=1=1^{10}=(-1)^{10}$
$\Rightarrow x-\frac{1}{2}=1$ hoặc $x-\frac{1}{2}=-1$
$\Rightarrow x=\frac{3}{2}$ hoặc $x=\frac{-1}{2}$

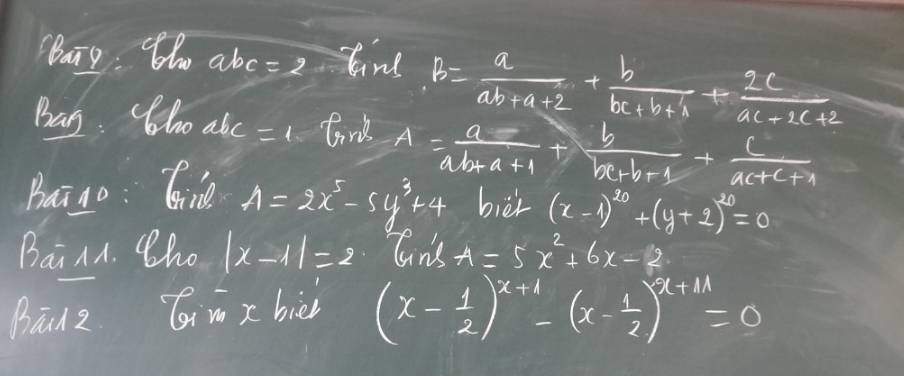












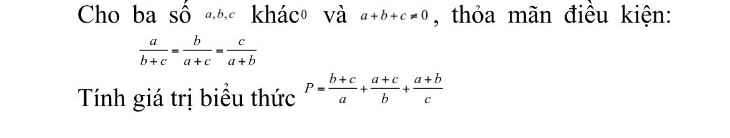

 với mọi người mik cần gấp mik cảm ơn nhìu
với mọi người mik cần gấp mik cảm ơn nhìu