Các câu hỏi tương tự
Miền nghiệm của hệ bất phương trình
x
-
y
≤
1
x
≥
1
y
≤
3
được biểu diễn là hình A.Tam giác B. Tứ giác C. Ngũ giác D. Lục giác
Đọc tiếp
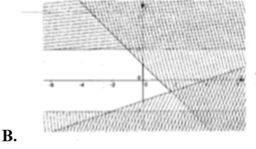
Miền nghiệm của hệ bất phương trình x - y ≤ 1 x ≥ 1 y ≤ 3 được biểu diễn là hình
A.Tam giác
B. Tứ giác
C. Ngũ giác
D. Lục giác
Gọi D là hình phẳng giới hạn bởi đồ thị hàm số
y
x
cung tròn có phương trình
y
6
-
x
2
(
6
≤
x
≤...
Đọc tiếp
Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = x cung tròn có phương trình y = 6 - x 2 ( 6 ≤ x ≤ 6 ) và trục hoành (phần gạch chéo trong hình vẽ). Tính thể tích V của vật thể xoay tròn sinh bởi hình phẳng D khi quay D quanh trục Ox.
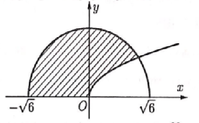
A. V = 8 π 6 - 2 π .
B. V = 8 π 6 + 22 π 3 .
C. V = 8 π 6 - 22 π 3 .
D. V = 4 π 6 + 22 π 3 .
Phần mặt phẳng không bị gạch (không kể bờ) là miền nghiệm của bất phương trình nào dưới đây A. 2x+y1 B. 2x+y1 C. 2x+y
≤
1
D. 2x+y
≥
1
Đọc tiếp
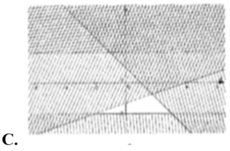
Phần mặt phẳng không bị gạch (không kể bờ) là miền nghiệm của bất phương trình nào dưới đây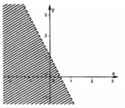
A. 2x+y<1
B. 2x+y>1
C. 2x+y ≤ 1
D. 2x+y ≥ 1
Cho hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi đường cong (P) có phương trình
y
1
4
x
2
. Gọi S là hình phẳng không bị gạch (như hình vẽ). Tính thể tích của vật thể tròn xoay khi cho phần qua quanh trục Ox A.
V
64
π
5
B.
V
...
Đọc tiếp
Cho hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi đường cong (P) có phương trình y = 1 4 x 2 . Gọi S là hình phẳng không bị gạch (như hình vẽ). Tính thể tích của vật thể tròn xoay khi cho phần qua quanh trục Ox
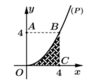
A. V = 64 π 5
B. V = 128 π 3
C. V = 128 π 5
D. V = 256 π 5
Cho hàm số y f(x) và hàm số bậc ba y g(x) có đồ thị như hình vẽ bên. Diện tích phần gạch chéo được tính bởi công thức nào sau đây?
A
.
S
∫
-
3
-
1
[
f
(
x
)
-
g
(
x
)
]
dx
+
∫
-
1...
Đọc tiếp
Cho hàm số y = f(x) và hàm số bậc ba y = g(x) có đồ thị như hình vẽ bên. Diện tích phần gạch chéo được tính bởi công thức nào sau đây?
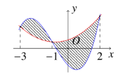
A . S = ∫ - 3 - 1 [ f ( x ) - g ( x ) ] dx + ∫ - 1 2 [ g ( x ) - f ( x ) ] dx
B . S = | ∫ - 3 2 [ f ( x ) - g ( x ) ] dx |
C. S = ∫ - 3 - 1 [ g ( x ) - f ( x ) ] dx + ∫ - 1 2 [ f ( x ) - g ( x ) ] dx
D. S = ∫ - 3 - 1 [ g ( x ) - f ( x ) ] dx + ∫ - 1 2 [ g ( x ) - f ( x ) ] dx
Trong hệ trục tọa độ Oxyz, cho Parabol
P
:
y
x
2
và hai đường thẳng
y
a
,
y
b
0
a
b
(hình vẽ). Gọi
S
1
là diện tích hình phẳng giới hạn bởi parabol (P) đường thẳn...
Đọc tiếp
Trong hệ trục tọa độ Oxyz, cho Parabol P : y = x 2 và hai đường thẳng y = a , y = b 0 < a < b (hình vẽ). Gọi S 1 là diện tích hình phẳng giới hạn bởi parabol (P) đường thẳng y = a và đường thẳng y = b (phần gạch chéo) và S 2 là diện tích hình phẳng giới hạn bởi parabol (P) và đường thẳng y = a (phần tô đậm). Với điều kiện nào sau đây của a và b thì S 1 = S 2
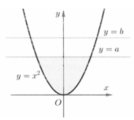
A. b = 4 a 3
B. b = 2 a 3
C. b = 3 a 3
D. b = 6 a 3
Tính diện tích S của miền hình phẳng giới hạn bởi đồ thị của hàm số
f
x
a
x
3
+
b
x
2
+
c
, các đường thẳng
x
−
1
,
x
2
và trục hoành (miền gạch chéo cho trong hình vẽ). A.
S
51
8
B...
Đọc tiếp
Tính diện tích S của miền hình phẳng giới hạn bởi đồ thị của hàm số f x = a x 3 + b x 2 + c , các đường thẳng x = − 1 , x = 2 và trục hoành (miền gạch chéo cho trong hình vẽ).
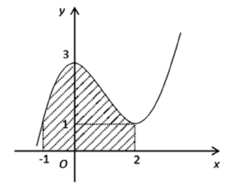
A. S = 51 8
B. S = 52 8
C. S = 50 8
D. S = 53 8
Cho (H) là hình phẳng giới hạn bởi parabol
y
3
x
2
và nửa đường tròn có phương trình
y
4
-
x
2
với
-
2
≤
x
≤
2
(phần tô đậm trong hình vẽ). Diện tích của (H) bằng A.
2
π
+
5...
Đọc tiếp
Cho (H) là hình phẳng giới hạn bởi parabol y = 3 x 2 và nửa đường tròn có phương trình y = 4 - x 2 với - 2 ≤ x ≤ 2 (phần tô đậm trong hình vẽ). Diện tích của (H) bằng
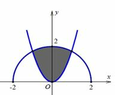
A. 2 π + 5 3 3
B. 4 π + 5 3 3
C. 4 π + 3 3
D. 2 π + 3 3
Cho
(
H
)
là hình phẳng giới hạn bởi parabol
y
3
x
2
và nửa đường tròn có phương trình
y
4
-
x
2
(với
-
2
≤
x
≤
2
) (phần tô đậm trong hình vẽ). Diện tích của
(
H
)
bằng A. ...
Đọc tiếp
Cho ( H ) là hình phẳng giới hạn bởi parabol y = 3 x 2 và nửa đường tròn có phương trình y = 4 - x 2 (với - 2 ≤ x ≤ 2 ) (phần tô đậm trong hình vẽ). Diện tích của ( H ) bằng
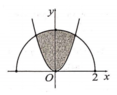
A. 2 π + 3 3
B. 4 π + 5 3 3
C. 2 π + 5 3 3
D. 4 π + 3 3