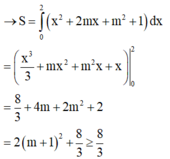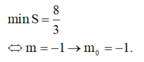Các câu hỏi tương tự
Biết hình phẳng giới hạn bởi đường thẳng y=x+3, trục hoành và đường thẳng x=m (m>0) có diện tích bằng 8. Khi đó giá trị m gần giá trị nào nhất trong các giá trị sau?
A. 0.
B. –2.
C. 3.
D. 5.
Cho (P)
y
x
2
+
1
và đường thẳng d: mx-y+20. Tìm m để diện tích hình phẳng giới hạn bởi (P) và d đạt giá trị nhỏ nhất: A. 0,5 B. 0,75 C. 1 D. 0
Đọc tiếp
Cho (P) y = x 2 + 1 và đường thẳng d: mx-y+2=0. Tìm m để diện tích hình phẳng giới hạn bởi (P) và d đạt giá trị nhỏ nhất:
A. 0,5
B. 0,75
C. 1
D. 0
Xét hình phẳng (H) được giới hạn bởi hàm số
y
x
2
, đường thẳng
y
k
2
với
0
≤
k
≤
1
; trục tung và đường thẳng x1. Biết (H) được chia thành hai phần có diện tích
S
1
S
2
như hình vẽ. Gọi...
Đọc tiếp
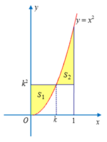
Xét hình phẳng (H) được giới hạn bởi hàm số y = x 2 , đường thẳng y = k 2 với 0 ≤ k ≤ 1 ; trục tung và đường thẳng x=1. Biết (H) được chia thành hai phần có diện tích S 1 S 2 như hình vẽ. Gọi k 1 , k 2 lần lượt là giá trị của k làm cho tổng S 1 + S 2 có giá trị lớn nhất và nhỏ nhất. Tính giá trị của T = k 1 + k 2
![]()
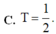
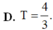
Diện tích hình phẳng giới hạn bởi đường cong
y
a
x
(a0), trục hoành và đường thẳng xa bằng
k
a
2
,
(
k
∈
ℝ
)
. Tính giá trị của tham số k.
Đọc tiếp
Diện tích hình phẳng giới hạn bởi đường cong y = a x (a>0), trục hoành và đường thẳng x=a bằng k a 2 , ( k ∈ ℝ ) . Tính giá trị của tham số k.
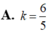
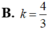
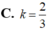
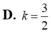
Cho hình phẳng (H) được giới hạn bởi đường cong
y
m
2
-
x
2
(m là tham số khác 0) và trục hoành. Khi (H) quay xung quanh trục hoành được khối tròn xoay có thể tích V. Có bao nhiêu giá trị nguyên của m để
V
1000
π
. A. 18. B. 20. C. 19. D. 21.
Đọc tiếp
Cho hình phẳng (H) được giới hạn bởi đường cong y = m 2 - x 2 (m là tham số khác 0) và trục hoành. Khi (H) quay xung quanh trục hoành được khối tròn xoay có thể tích V. Có bao nhiêu giá trị nguyên của m để V < 1000 π .
A. 18.
B. 20.
C. 19.
D. 21.
Gọi (H) là hình phẳng giới hạn bởi parabol y
(
x
-
3
)
2
trục hoành và trục tung. Gọi k1,k2(k1k2) lần lượt là hệ số góc của đường thẳng qua điểm A(0;9 và chia (H) thành ba hình mặt phẳng có diện tích bằng nhau( tham khảo hình vẽ bên). Giá trị của k1-k2 bằng
Đọc tiếp
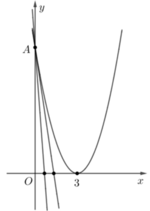
Gọi (H) là hình phẳng giới hạn bởi parabol
y= ( x - 3 ) 2 trục hoành và trục tung. Gọi k1,k2(k1>k2) lần lượt là hệ số góc của đường thẳng qua điểm A(0;9 và chia (H) thành ba hình mặt phẳng có diện tích bằng nhau( tham khảo hình vẽ bên). Giá trị của k1-k2 bằng

![]()
![]()
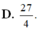
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số:
y
x
2
-
6
x
+
9
và 2 đường thẳng x 0; y 0 Đường thẳng (d) có hệ số k và cắt trục tung tại điểm A(0;4). Giá trị của k để (d) chia (H) thành 2 phần có diện tích bằng nhau là:
Đọc tiếp
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số: y = x 2 - 6 x + 9 và 2 đường thẳng x = 0; y = 0 Đường thẳng (d) có hệ số k và cắt trục tung tại điểm A(0;4). Giá trị của k để (d) chia (H) thành 2 phần có diện tích bằng nhau là:
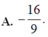
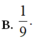
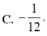
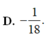
Trong mặt phẳng Oxy, cho prabol (P)
y
x
2
. Viết phương trình đường thẳng d đi qua M(1;3) sao cho diện tích hình phẳng giới hạn bởi (P) và d đạt giá trị nhỏ nhất.
Đọc tiếp
Trong mặt phẳng Oxy, cho prabol (P) y = x 2 . Viết phương trình đường thẳng d đi qua M(1;3) sao cho diện tích hình phẳng giới hạn bởi (P) và d đạt giá trị nhỏ nhất.
![]()
![]()
![]()
![]()
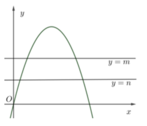
Gọi H là hình phẳng giới hạn bởi đồ thị hàm số
y
-
x
2
+
4
x
và trục hoành. Hai đường thẳng ym và yn chia thành 3 phần có diện tích bằng nhau (tham khảo hình vẽ). Giá trị biểu thức
T
(
4
-
m
)
3
+...
Đọc tiếp
Gọi H là hình phẳng giới hạn bởi đồ thị hàm số y = - x 2 + 4 x và trục hoành. Hai đường thẳng y=m và y=n chia thành 3 phần có diện tích bằng nhau (tham khảo hình vẽ). Giá trị biểu thức T = ( 4 - m ) 3 + ( 4 - n ) 3 bằng
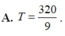
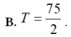
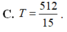
![]()