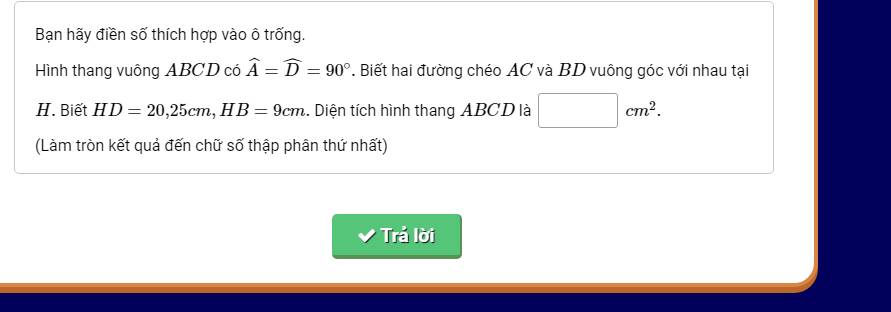
Xét ΔABD vuông tại A có AH là đường cao
nên \(AH^2=HD\cdot HB\)
=>\(AH=\sqrt{20,25\cdot9}=13,5\left(cm\right)\)
Xét ΔDAC vuông tại D có DH là đường cao
nên \(DH^2=AH\cdot HC\)
=>\(HC=\dfrac{20.25^2}{13.5}=30,375\left(cm\right)\)
BD=BH+DH=9+20,25=29,25(cm)
AC=AH+HC=13,5+30,375=43,875(cm)
Vì AC\(\perp\)BD tại H
nên \(S_{ABCD}=\dfrac{1}{2}\cdot AC\cdot BD=\dfrac{1}{2}\cdot29,25\cdot43,875\simeq641,7\left(cm^2\right)\)









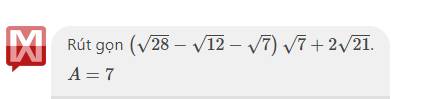 tại sao rú gọn lại ra kết quả nnay ạ gthich giúp e
tại sao rú gọn lại ra kết quả nnay ạ gthich giúp e







