a: \(\dfrac{2x^3+5x^2-2x+3}{2x^2-x+1}\)
\(=\dfrac{2x^3-x^2+x+6x^2-3x+3}{2x^2-x+1}\)
\(=\dfrac{x\left(2x^2-x+1\right)+3\left(2x^2-x+1\right)}{2x^2-x+1}\)
=x+3
b: \(\dfrac{2x^3-5x^2+6x-15}{2x-5}\)
\(=\dfrac{x^2\left(2x-5\right)+3\left(2x-5\right)}{2x-5}\)
\(=x^2+3\)
c: \(\dfrac{x^4-x-14}{x-2}\)
\(=\dfrac{x^4-2x^3+2x^3-4x^2+4x^2-8x+7x-14}{x-2}\)
\(=\dfrac{x^3\left(x-2\right)+2x^2\left(x-2\right)+4x\left(x-2\right)+7\cdot\left(x-2\right)}{x-2}\)
\(=x^3+2x^2+4x+7\)
Đúng 1
Bình luận (0)
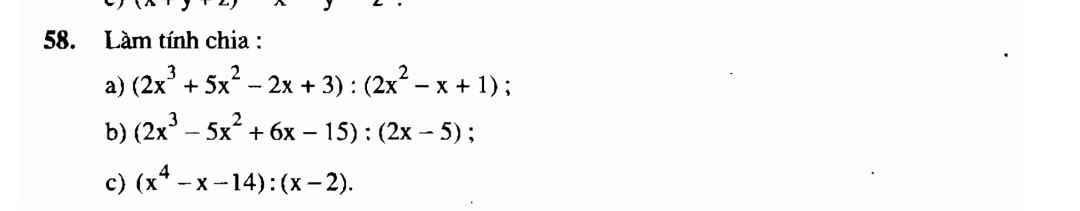
mng ơi giúp em với ạ! e đag cần gấp! e cảm ơn mng nhiều lắmm <33 
lm giúp mk bài 3 với bài 4 với ạ, mk đng cần gấp, cảm ơn mn rất rất nhiều ạ !!!!
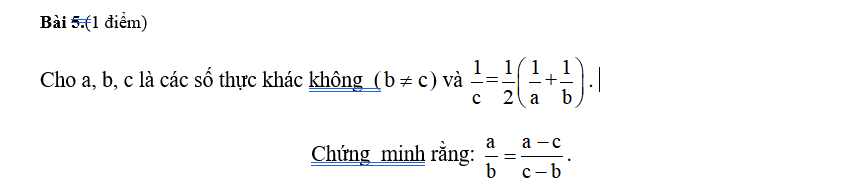
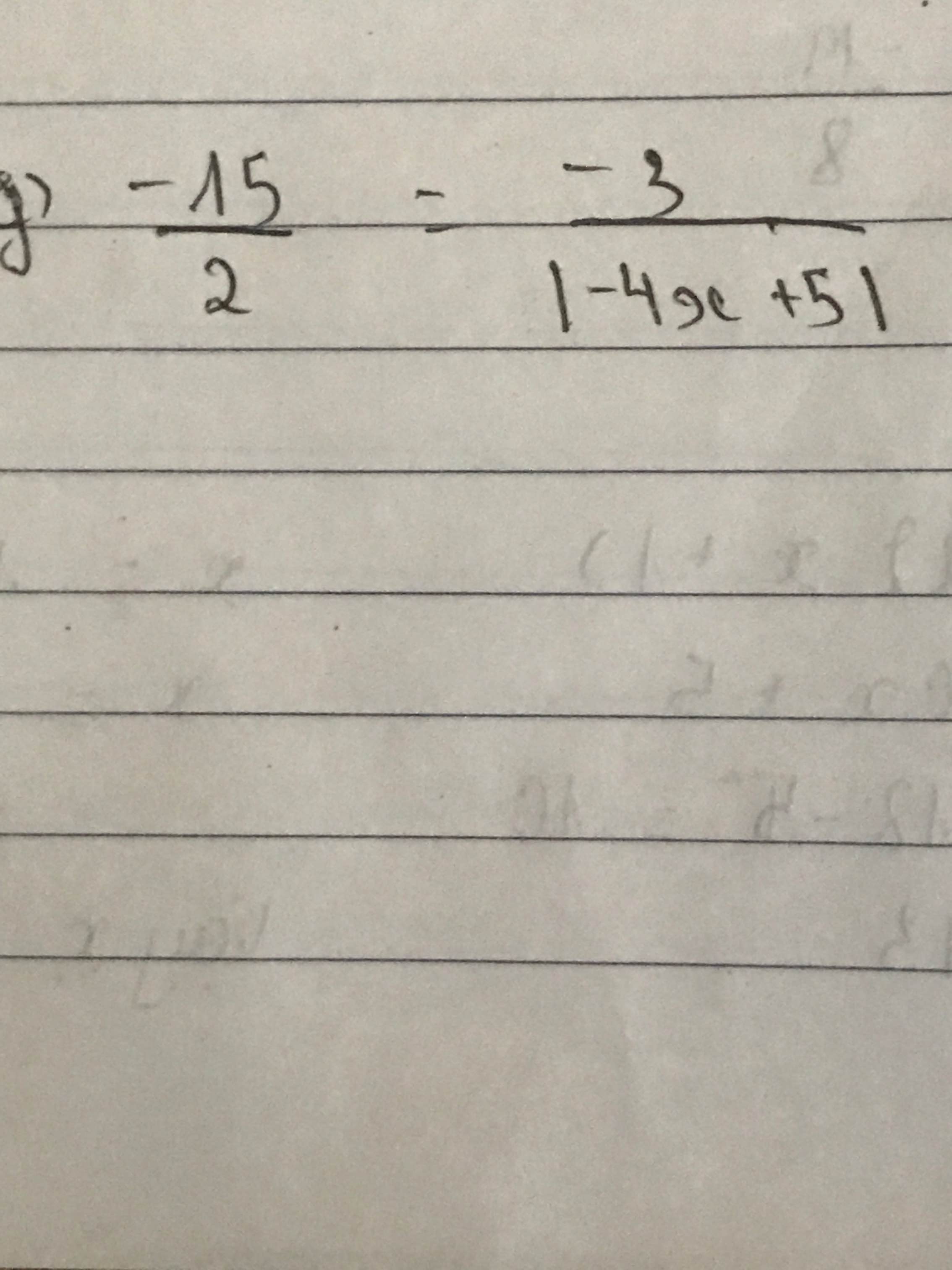
giúp mik vs ạ mik đag cần gấp pls