Đường thẳng AB nhận 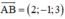 là 1 vtcp và đi qua A(1; 0; -3)
là 1 vtcp và đi qua A(1; 0; -3)
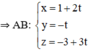
Đường thẳng AB nhận 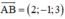 là 1 vtcp và đi qua A(1; 0; -3)
là 1 vtcp và đi qua A(1; 0; -3)
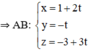
Trong không gian Oxyz, cho ba điểm A(1; 2; 0), B(-2; 1; 3), C(7; -3; -6). Viết phương trình tham số của đường thẳng d đi qua trọng tâm G của tam giác ABC, đồng thời d song song với hai mặt phẳng (Oxy) và (Oxz)
A. x = 2 + t, y = 0, z = -1
B. x = -2 + t, y = 0, z = -1
C. x = 1 + 2t, y = 0, z = -t
D. x = 6 + t, y = 0, z = -3
Lập phương trình mặt phẳng ( α ) đi qua hai điểm A(0; 1; 0) , B(2; 3; 1) và vuông góc với mặt phẳng ( β ): x + 2y – z = 0 .
Lập phương trình tham số của đường thẳng d đi qua điểm M 0 x 0 , y 0 , z 0 và song song với hai mặt phẳng cắt nhau
(P) Ax + By + Cz + D = 0 và (Q): A’x + B’y + C’z + D’ = 0
Lập phương trình mặt phẳng (α) qua hai điểm A(1; 0; 1), B(5; 2; 3) và vuông góc với mặt phẳng ( β) : 2x – y + z – 7 = 0
Viết phương trình tham số, phương trình chính tắc của đường thẳng ∆ trong các trường hợp sau: ∆ đi qua điểm B(1; 0; -1) và vuông góc với mặt phẳng ( α ) : 2x – y + z + 9 = 0
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d đi qua điểm A(1; 2; 3) và vuông góc với mặt phẳng (α): 4x + 3y - 7z + 1 = 0. Phương trình tham số của d là:
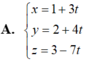

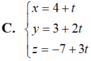
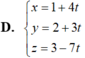
Trong không gian Oxyz, viết phương trình tham số của đường thẳng d đi qua điểm M(1;2;-3) và d vuông góc với mặt phẳng (P): 3x + y + 1 = 0
A. x = -1 - 3t, y = -2 - t, z = 3
B. x = 1 + 3t, y = 2 + t, z = -3 + t
C. x = 3 + t, y = 1 + 2t, z = -3t
D. x = 1 + 3t, y = 2 + t, z = -3
Lập phương trình tham số của đường thẳng d đi qua điểm M 0 x 0 , y 0 , z 0 và vuông góc với mặt phẳng (P): Ax + By + Cz + D = 0.
Viết các phương trình (tham số và chính tắc) của các đường thẳng sau:
a) Các trục tọa độ Ox, Oy và Oz.
b) Các đường thẳng đi qua điểm M0 (x0,y0,z0) (với x0y0z0 ≠ 0) và song song với mỗi trục tọa độ.
c) Đường thẳng đi qua M(2; 0; -1) và có vectơ chỉ phương u→(0,0,-3)
d) Đường thẳng đi qua N(-2, 1, 2) và vectơ chỉ phương u→=(-1,3,5)
e) Đường thẳng đó qua N(3, 2, 1) và vuông góc với mặt phẳng: 2x-5y+4=0
f) Đường thẳng đi qua hai điểm P(2, 3, -1) và Q(1, 2, 4).