Đáp án A
Kẻ A P ⊥ B C tan 60 ∘ = A ' A A P
⇒ A ' A = A P 3 = 3 . a 3 2 = 3 a 2 ⇒ V A B C C ' B ' = 2 V B ' . A B C = 2. 1 3 B B ' . S A B C = 2 3 . 3 a 2 . a 2 3 4 = a 3 3 4
Đáp án A

Kẻ A P ⊥ B C tan 60 ∘ = A ' A A P
⇒ A ' A = A P 3 = 3 . a 3 2 = 3 a 2 ⇒ V A B C C ' B ' = 2 V B ' . A B C = 2. 1 3 B B ' . S A B C = 2 3 . 3 a 2 . a 2 3 4 = a 3 3 4
Cho lăng trụ tam giác ABC.A′B′C′ có độ dài cạnh bên bằng 4 và khoảng cách từ điểm A đến các đường thẳng BB′,CC′ lần lượt bằng 1 và 2. Biết góc giữa hai mặt phẳng (ABB′A′) và (ACC′A′) bằng 60 ° . Tính thể tích khối lăng trụ ABC.A′B′C′.
A. 4 3
B. 3
C. 3 3
D. 2 3
Cho hình lăng trụ tam giác đều ABC.A′B′C′ có góc giữa hai mặt phẳng (A′BC) và (ABC) bằng 60 0 , cạnh AB = 2. Thể tích V của khối lăng trụ ABC.A′B′C′ là
A. 3 3 4
B. 3
C. 3
D. 3 3
Cho lăng trụ đứng ABC.A′B′C′ có đáy là tam giác vuông, AB=AC=a. Góc giữa hai mặt phẳng (ACC′),(AB′C′) bằng 60 ° . Thể tích của khối chóp B′.ACC′A′ bằng
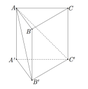
A. a 3 2 12
B. a 3 2 6
C. a 3 2 36
D. a 3 2 18
Cho khối đa diện như hình vẽ bên. Trong đó ABC.A' B' C' là khối lăng trụ tam giác đều có tất cả các cạnh đều bằng 1, S.ABC khối chóp tam giác đều có cạnh bên SA=2/3. Mặt phẳng (SA' B' ) chia khối đa diện đã cho thành hai phần. Gọi V 1 là thể tích phần khối đa diện chứa đỉnh A, V 2 là thể tích phần khối đa diện không chứa đỉnh A. Mệnh đề nào sau đây đúng
A. 72 V 1 = 5 V 2
B. 3 V 1 = V 2
C. 24 V 1 = 5 V 2
D. 4 V 1 = 5 V 2
Cho khối lăng trụ tam giác đều ABC.A′B′C′ có cạnh đáy bằng a, góc giữa đường thẳng B′C và mặt đáy bằng 30 ° . Khoảng cách giữa hai đường thẳng A′C và B′C′ bằng
A. a 15 15
B. a 15 5
C. a 3 13
D. a 39 13
Cho khối lăng trụ tam giác đều ABC.A′B′C′ có cạnh đáy bằng a, góc giữa đường thẳng B′C và mặt đáy bằng 30 ° . Khoảng cách giữa hai đường thẳng A′C và B′C′ bằng
A. a 15 15
B. a 15 5
C. a 3 13
D. a 39 13
Cho khối lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a và điểm A’ cách đều ba điểm A, B, C. Cạnh bên AA’ tạo với mặt phẳng đáy một góc 60 ° Tính thể tích khối lăng trụ ABC.A’B’C’
A. a 3 3 10
B. a 3 3 12
C. a 3 3 4
D. a 3 3 8
Cho khối lăng trụ ABC.A′B′C′ có đáy là tam giác vuông cân tại A, BC = 2a và hình chiếu vuông góc của A′ lên mặt phẳng (ABC) trùng với trung điểm cạnh BC, góc giữa AA′ và mặt đáy bằng 60 ° . Thể tích khối lăng trụ đã cho bằng
A. 3 a 3 3
B. a 3 2
C. 3 a 3 2
D. 3 a 3
Cho khối lăng trụ tam giác đều ABC.A′B′C′ có tất cả các cạnh bằng a.Gọi M, N lần lượt là trung điểm của AB, B′C′. Mặt phẳng (A′MN) cắt cạnh BC tại P. Thể tích của khối đa diện MBP.A′B′N bằng
A. 7 a 3 3 32
B. a 3 3 32
C. 7 a 3 3 68
D. 7 a 3 3 96
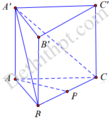
Cho hình lăng trụ ABC A'B'C' có AA'=a, góc giữa cạnh bên và mặt đáy bằng 60°. Tam giác ABC vuông tại C và góc B A C ^ = 60 ° . Hình chiếu vuông góc của B' lên mặt phẳng A B C trùng với trọng tâm của Δ A B C . Tính thể tích khối tứ diện A'ABC theo a
A. V A ' A B C = 3 a 3 208
B. V A ' A B C = 27 a 3 208
C. V A ' A B C = 81 a 3 208
D. V A ' A B C = 9 a 3 208