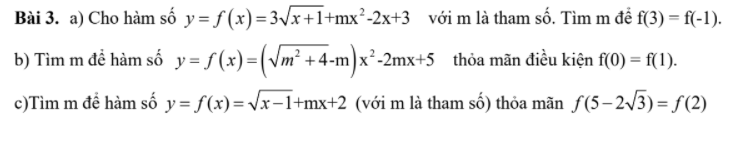Question

Làm ơn giúp mình với ạ! MÌNH CẦN GẤP😔

Answer 1

Bài 13:

$6-2\sqrt{5}=5-2\sqrt{5}.\sqrt{1}+1$

$=(\sqrt{5}-1)^2$

Tương tự: $6+2\sqrt{5}=(\sqrt{5}+1)^2$
Do đó:
$M=\sqrt{(\sqrt{5}+1)^2}-\sqrt{(\sqrt{5}-1)^2}$

$=|\sqrt{5}+1|-|\sqrt{5}-1|=(\sqrt{5}+1)-(\sqrt{5}-1)$

$=2$

Answer 2

Bài 14:

a.

$M=\sqrt{4+2\sqrt{4}.\sqrt{5}+5}-\sqrt{4-2\sqrt{4}.\sqrt{5}+5}$

$=\sqrt{(\sqrt{4}+\sqrt{5})^2}-\sqrt{(\sqrt{4}-\sqrt{5})^2}$

$=|\sqrt{4}+\sqrt{5}|-|\sqrt{4}-\sqrt{5}|$

$=2+\sqrt{5}-(\sqrt{5}-2)=4$

b.

$N=\sqrt{7-2\sqrt{7}+1}-\sqrt{7+2\sqrt{7}+1}$

$=\sqrt{(\sqrt{7}-1)^2}-\sqrt{(\sqrt{7}+1)^2}$

$=|\sqrt{7}-1|-|\sqrt{7}+1|$

$=(\sqrt{7}-1)-(\sqrt{7}+1)=-2$

 

Answer 3

Bài 15:

a.

$P=\sqrt{3^2+2.3\sqrt{2}+2}-\sqrt{3^2-2.3\sqrt{2}+2}$

$=\sqrt{(3+\sqrt{2})^2}-\sqrt{(3-\sqrt{2})^2}$

$=|3+\sqrt{2}|-|3-\sqrt{2}|$

$=3+\sqrt{2}-(3-\sqrt{2})=2\sqrt{2}$

b,

$Q=\sqrt{9+2\sqrt{9.8}+8}+\sqrt{9-2\sqrt{9.8}+8}$

$=\sqrt{(\sqrt{9}+\sqrt{8})^2}+\sqrt{(\sqrt{9}-\sqrt{8})^2}$

$=|3+\sqrt{8}|+|3-\sqrt{8}|$

$=3+\sqrt{8}+(3-\sqrt{8})=6$

Answer 4

Bài 16:

a. $A=\sqrt{64a^2}+2a=\sqrt{(8a)^2}+2a$
$=|8a|+2a$

$A=-8a+2a=-6a$ nếu $a<0$

$A=8a+2a=10$ nếu $a\geq 0$

b.

$B=3\sqrt{9a^6}-6a^3=3\sqrt{(3a^3)^2}-6a^3$

$=3|3a^3|-6a^3=9|a^3|-6a^3$

$B=9a^3-6a^3=3a^3$ nếu $a\geq 0$

$B=-9a^3-6a^3=-15a^3$ nếu $a< 0$

Answer 5

Bài 17:

a.

$A=\sqrt{(a+3)^2}+\sqrt{(a-3)^2}$
$=|a+3|+|a-3|$

$=a+3+(3-a)=6$

b.

$B=\sqrt{(a-1)+2\sqrt{a-1}+1}+\sqrt{(a-1)-2\sqrt{a-1}+1}$

$=\sqrt{(\sqrt{a-1}+1)^2}+\sqrt{(\sqrt{a-1}-1)^2}$

$=|\sqrt{a-1}+1|+|\sqrt{a-1}-1|$

$=\sqrt{a-1}+1+1-\sqrt{a-1}=2$