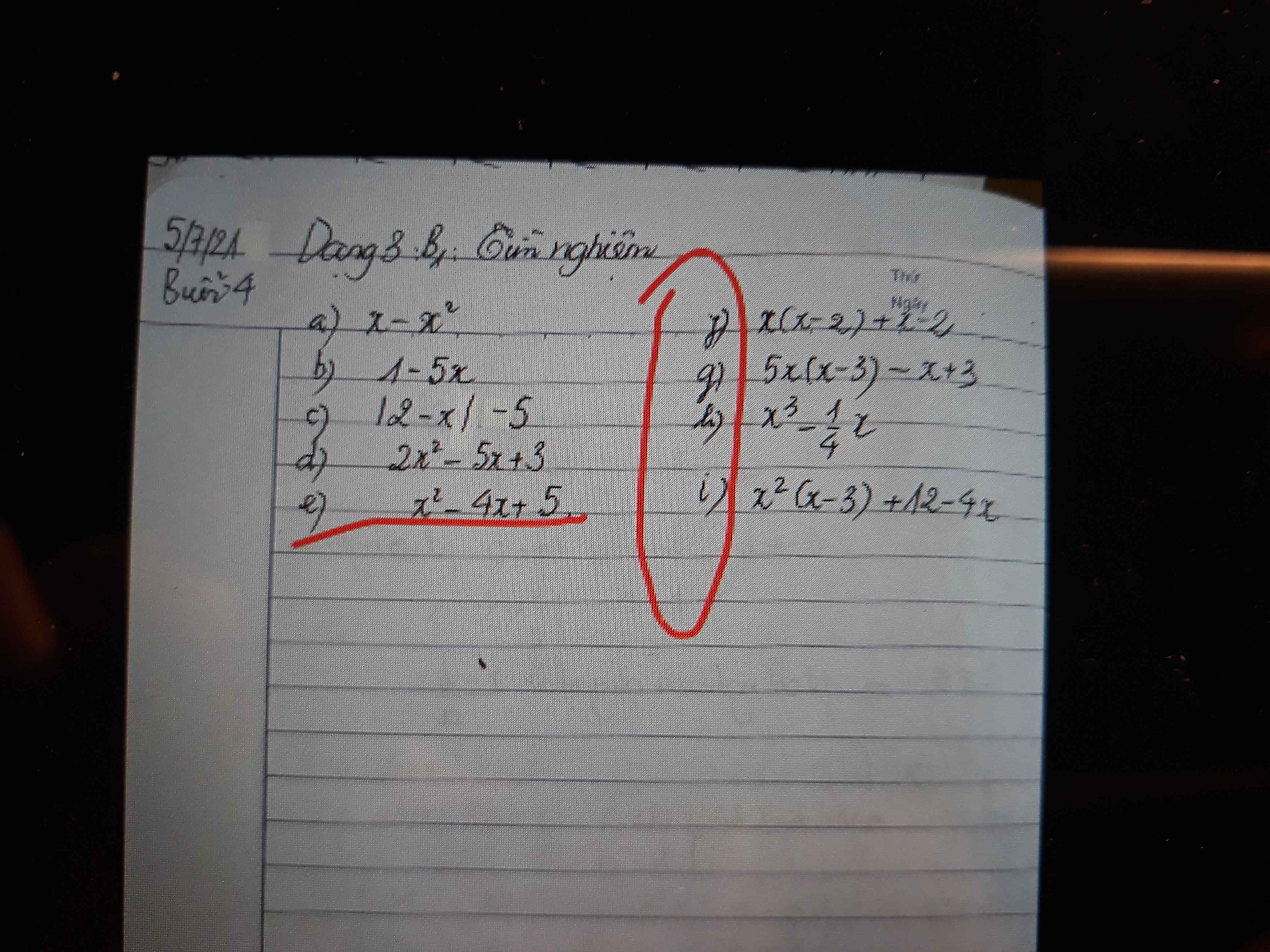Bài 4:
b. Ta có:
$(2-x)^2\geq 0$ với mọi $x$
$(y-1)^2\geq 0$ với mọi $y$
$\Rightarrow B=(2-x)^2+2(y-1)^2-5\geq 0+2.0-5=-5$
Vậy $B_{\min}=-5$. Giá trị này đạt tại $2-x=y-1=0$
$\Lefrightarrow x=2; y=1$
c.
Ta thấy: $(4x+1)^2\geq 0$ với mọi $x$
$\Rightarrow 3-(4x+1)^2\leq 3$
$\Rightarrow C=\frac{5}{3-(4x+1)^2}\geq \frac{5}{3}$
Vậy $C_{\min}=\frac{5}{3}$. Giá trị này đạt tại $4x+1=0\Leftrightarrow x=\frac{-1}{4}$
Bài 5:
c.
Vì:
$(2x+1)^2\geq 0$ với mọi $x$
$(y-3,5)^2\geq 0$ với mọi $y$
$\Rightarrow -P= (2x+1)^2+7(y-3,5)^2-\frac{2}{3}\geq 0+7.0-\frac{2}{3}=\frac{-2}{3}$
$\Rightarrow P\leq \frac{2}{3}$
Vậy $P_{\max}=\frac{2}{3}$. Giá trị này đạt tại $2x+1=y-3,5=0$
$\Leftrightarrow x=\frac{-1}{2}; y=3,5$
Bài 6:
\(\text{VT}=\frac{2-1}{1.2}+\frac{4-3}{3.4}+\frac{6-5}{5.6}+....+\frac{100-99}{99.100}\)
\(=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+...+\frac{1}{99}-\frac{1}{100}\)
\(=(1+\frac{1}{3}+\frac{1}{5}+...+\frac{1}{99})-(\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+...+\frac{1}{100})\)
\(=(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+...+\frac{1}{99}+\frac{1}{100})-2(\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+...+\frac{1}{100})\)
\(=(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+...+\frac{1}{99}+\frac{1}{100})-(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{50})\)
\(=\frac{1}{51}+\frac{1}{52}+...+\frac{1}{100}\)