bài 1:
1) Thay x = 64 vào A, ta có:
\(A=\dfrac{2+\sqrt[]{64}}{\sqrt[]{64}}=\dfrac{2+8}{8}=\dfrac{10}{8}=\dfrac{5}{4}\)
Vậy khi x = 64 thì A = \(\dfrac{5}{4}\)
2) \(B=\dfrac{\sqrt[]{x}-1}{\sqrt[]{x}}+\dfrac{2\sqrt[]{x}+1}{x+\sqrt[]{x}}\)
\(=\dfrac{\left(\sqrt[]{x}-1\right)\left(x+\sqrt[]{x}\right)}{\sqrt[]{x}\left(x+\sqrt[]{x}\right)}+\dfrac{\sqrt[]{x}\left(2\sqrt[]{x}+1\right)}{\sqrt[]{x}\left(x+\sqrt[]{x}\right)}\)
\(=\dfrac{\left(\sqrt[]{x}-1\right)\left(x+\sqrt[]{x}\right)+\sqrt[]{x}\left(2\sqrt[]{x}+1\right)}{\sqrt[]{x}\left(x+\sqrt[]{x}\right)}\)
\(=\dfrac{x\sqrt{x}+x-x-\sqrt{x}+2x+\sqrt{x}}{\sqrt{x}\left(x+\sqrt{x}\right)}\)
\(=\dfrac{x\sqrt{x}+2x}{x\sqrt{x}+x}\)
\(=\dfrac{x\left(\sqrt[]{x}+2\right)}{x\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt[]{x}+2}{\sqrt{x}+1}\)
3) \(\dfrac{A}{B}>\dfrac{3}{2}\)
⇔ \(\dfrac{2+\sqrt{x}}{\sqrt{x}}:\dfrac{\sqrt[]{x}+2}{\sqrt{x}+1}>\dfrac{3}{2}\)
⇔ \(\dfrac{2+\sqrt{x}}{\sqrt{x}}.\dfrac{\sqrt{x}+1}{\sqrt{x}+2}>\dfrac{3}{2}\)
⇔ \(\dfrac{\sqrt{x}+1}{\sqrt{x}}>\dfrac{3}{2}\)
⇔ \(\dfrac{2\sqrt{x}+2}{2\sqrt{x}}>\dfrac{3\sqrt{x}}{2\sqrt{x}}\)
⇒ \(2\sqrt{x}+2>3\sqrt[]{x}\)
⇔ \(\sqrt{x}< 2\)
⇔ \(x< 4\)
Kết hợp với điều kiện đầu bài, vậy để \(\dfrac{A}{B}>\dfrac{3}{2}\) thì \(x\in\left\{1;2;3\right\}\)
Bài 3:
1) \(\left\{{}\begin{matrix}3\left(x+1\right)+2\left(x+2y\right)=4\\4\left(x+1\right)-\left(x+2y\right)=9\end{matrix}\right.\)
Đặt \(a=x+1;b=x+2y\)
Hệ pt trở thành: \(\left\{{}\begin{matrix}3a+2b=4\\4a-b=9\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}3a+2b=4\\8a-2b=18\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}11a=22\\3a+2b=4\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}a=2\\6+2b=4\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}a=2\\b=-1\end{matrix}\right.\)
\(x+1=2\) ⇒ \(x=1\)
\(x+2y=-1\) hay \(1+2y=-1\) ⇒ \(y=-1\)
Vậy hệ pt có nghiệm duy nhất \(\left(1;-1\right)\)
2) chưa học:)))
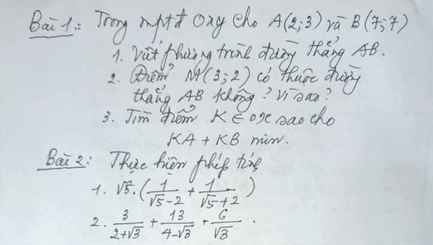làm hộ mik bài 1 thôi nha
