Làm giúp mik hết 4 bài này với ạ, mik cảm ơn
Câu 1 (1,5 điểm) Tính:
a) \( 15 + 23 + (-25) + (-23) \).
b) \( 6^5 \cdot 6^3 - 8 \).
c) \( 31 \cdot (-18) + 31 \cdot (-81) - 31 \).
Câu 2 (1,5 điểm) Tìm \( x \), biết:
a) \( 2x - 35 = 15 \).
b) \( (2x - 5) + 17 = 6 \).
Câu 3 (1,5 điểm)
Một số sách khi xếp thành từng bó 10 cuốn, 12 cuốn, 15 cuốn, 18 cuốn đều vừa đủ bó. Biết số sách trong khoảng 500 đến 800. Tìm số sách.
Câu 4 (2 điểm)
Bác Nam có một mảnh đất dạng hình chữ nhật có kích thước như hình vẽ. Bác dự định trồng rau trên khu vực hình \( AMCN \) và trồng hoa ở phần còn lại. Tiền công để trả cho mỗi mét vuông trồng hoa là 52 nghìn đồng, trồng rau là 58 nghìn đồng. Tính số tiền công cần chi trả để trồng hoa và rau.
Câu 1:
a: \(15+23+\left(-25\right)+\left(-23\right)\)
\(=\left(15-25\right)+\left(23-23\right)\)
=-10+0
=-10
b: \(6^5:6^3-8=6^2-8=36-8=28\)
c: \(31\cdot\left(-18\right)+31\cdot\left(-81\right)-31\)
\(=31\left(-18-81-1\right)\)
\(=31\cdot\left(-100\right)=-3100\)
Câu 2:
a: \(2x-35=15\)
=>2x=35+15=50
=>\(x=\dfrac{50}{2}=25\)
b: (2x-5)+17=6
=>2x+12=6
=>2x=6-12=-6
=>x=-3
Câu 4:
ΔABM vuông tại B
=>\(S_{BAM}=\dfrac{1}{2}\cdot BA\cdot BM=\dfrac{1}{2}\cdot8\cdot12=48\left(m^2\right)\)
ABCD là hình chữ nhật
=>AB=CD
mà AB=12m
nên CD=12m
ΔCDN vuông tại D
=>\(S_{DCN}=\dfrac{1}{2}\cdot DC\cdot DN=\dfrac{1}{2}\cdot12\cdot8=48\left(m^2\right)\)
ABCD là hình chữ nhật
=>\(S_{ABCD}=BC\cdot AB=16\cdot12=192\left(m^2\right)\)
Diện tích đất trồng hoa là:
\(48+48=96\left(m^2\right)\)
Diện tích đất trồng rau là:
\(192-96=96\left(m^2\right)\)
Số tiền cần bỏ ra để trồng hoa là:
\(96\cdot52=4992\left(nghìnđồng\right)\)
Số tiền cần bỏ ra để trồng rau là:
\(96\cdot58=5568\)(nghìn đồng)
Câu 3:
Gọi số sách là x(quyển)
(Điều kiện: \(x\in Z^+\))
\(10=2\cdot5;12=2^2\cdot3;15=3\cdot5;18=2\cdot3^2\)
=>\(BCNN\left(10;12;15;18\right)=2^2\cdot3^2\cdot5=180\)
Vì số sách khi xếp thành từng bó 10 cuốn; 12 cuốn; 15 cuốn; 18 cuốn thì đều vừa đủ nên \(x\in BC\left(10;12;15;18\right)\)
=>\(x\in B\left(180\right)\)
mà 500<=x<=800
nên \(x\in\left\{540;720\right\}\)
Vậy: Số sách có thể là 540 quyển hoặc 720 quyển









 2 bài này các bạn giúp mik phần d,e,f với
2 bài này các bạn giúp mik phần d,e,f với  còn bài này các bạn giúp mik phần c, h
còn bài này các bạn giúp mik phần c, h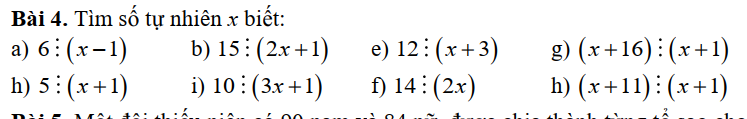 bài này các bạn giúp mik phần g, h, i
bài này các bạn giúp mik phần g, h, i các bạn giúp mik hết luôn hai bài này nhé, mik đang cần cực kì gấp
các bạn giúp mik hết luôn hai bài này nhé, mik đang cần cực kì gấp







