a.
Xét hai tam giác ABN và ACM có:
\(\left\{{}\begin{matrix}AB=AC\left(gt\right)\\\widehat{A}\text{ là góc chung}\\An=AM\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABN=\Delta ACM\left(c.g.c\right)\)
\(\Rightarrow BN=CM\)
b.
Do \(AB=AC\Rightarrow\Delta ABC\) cân tại A
\(\Rightarrow\widehat{B}=\widehat{C}\)
Lại có: \(\left\{{}\begin{matrix}AB=AC\left(gt\right)\\AM=AN\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow AB-AM=AC-AN\Rightarrow BM=CN\)
Xét hai tam giác BMC và CNB có:
\(\left\{{}\begin{matrix}BM=CN\left(cmt\right)\\\widehat{B}=\widehat{C}\left(cmt\right)\\BC\text{ là cạnh chung}\end{matrix}\right.\) \(\Rightarrow\Delta BMC=\Delta CNB\left(c.g.c\right)\)
\(\Rightarrow\widehat{BMC}=\widehat{CNB}\) hay \(\widehat{BMI}=\widehat{CNI}\)
Lại có \(\widehat{BIM}=\widehat{CIN}\) (đối đỉnh) \(\Rightarrow\widehat{IBM}=\widehat{ICN}\)
Xét hai tam giác BIM và CIN có:
\(\left\{{}\begin{matrix}\widehat{BMI}=\widehat{CNI}\left(cmt\right)\\BM=CN\left(cmt\right)\\\widehat{IBM}=\widehat{ICN}\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\Delta BIM=\Delta CIN\left(c.g.c\right)\)
c.
Từ \(\Delta BIM=\Delta CIN\Rightarrow IM=IN\)
Xét hai tam giác AIM và AIN có:
\(\left\{{}\begin{matrix}AM=AN\left(gt\right)\\IM=IN\left(cmt\right)\\AI\text{ là cạnh chung}\end{matrix}\right.\)
\(\Rightarrow\Delta AIM=\Delta AIN\left(c.c.c\right)\)
\(\Rightarrow\widehat{MAI}=\widehat{NAI}\)
\(\Rightarrow AI\) là phân giác của góc \(\widehat{A}\)
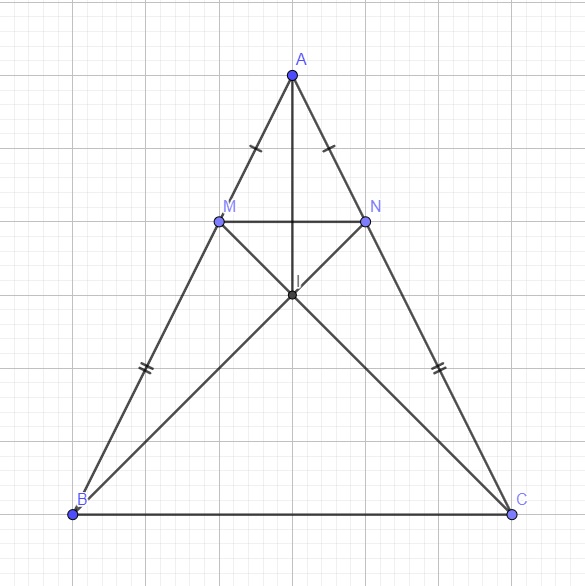
vẽ hình bài6 và làm 2 bài này giúp ạ 
