b.
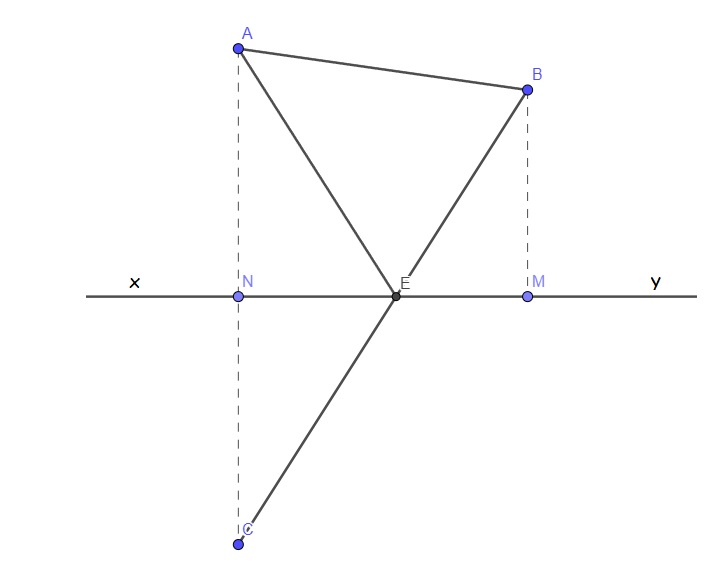
Do vận tốc của vận động viên là ko đổi nên thời gian chuyển động của VĐV là nhỏ nhất khi quãng đường chuyển động \(AE+BE\) của VĐV là ngắn nhất.
Gọi C là điểm đối xứng với A qua xy \(\Rightarrow xy\) là đường trung trực của AC
Do E thuộc xy \(\Rightarrow AE=CE\)
\(\Rightarrow AE+BE=CE+BE\ge BC\)
Dấu "=" xảy ra khi và chỉ khi E là giao điểm của BC và xy
C đối xứng A qua xy nên \(CN=AN=24\left(m\right)\)
Do \(BM||CN\) (cùng vuông góc xy), áp dụng định lý Thales:
\(\dfrac{EN}{EM}=\dfrac{CN}{BM}=\dfrac{24}{16}=\dfrac{3}{2}\)
\(\Rightarrow EN=\dfrac{3}{2}EM\)
Mà \(EN+EM=MN=30\left(m\right)\)
\(\Rightarrow\dfrac{3}{2}EM+EM=30\Rightarrow EM=12m\)
\(\Rightarrow EN=18m\)
\(\Rightarrow E\) là điểm nằm trên MN sao cho \(EM=12\left(m\right)\) và \(EN=18\left(m\right)\)
Khi đó:
\(\left(AE+BE\right)_{min}=BC=EC+EB=\sqrt{EN^2+CN^2}+\sqrt{EM^2+BM^2}=50\left(m\right)\)
\(\Rightarrow t=\dfrac{50}{6}=\dfrac{25}{3}\left(s\right)\)