Các câu hỏi tương tự
Một hình hộp chữ nhật có độ dài ba cạnh cùng xuất phát từ một đỉnh lần lượt là 2, 3, 4. Khi đó thể tích của hình hộp chữ nhật đó là:
A. 12.
B. 24.
C. 8.
D. 4.
Thể tích của khối hộp chữ nhật có độ dài các cạnh bằng a, b, c là A.
1
6
abc B.
1
2
abc C. abc D.
1
3
abc
Đọc tiếp
Thể tích của khối hộp chữ nhật có độ dài các cạnh bằng a, b, c là
A. 1 6 abc
B. 1 2 abc
C. abc
D. 1 3 abc
Cho khối hộp chữ nhật ABCD.ABCD. Gọi M là trung điểm của BB. Mặt phẳng (MDC) chia khối hộp chữ nhật thành hai khối đa diện, một khối chứa đỉnh C và một khối chứa đỉnh A. Gọi
V
1
,
V
2
lần lượt là thể tích hai khối đa diện chứa C và A. Tính
V
1
V
2
.
Đọc tiếp
Cho khối hộp chữ nhật ABCD.A'B'C'D'. Gọi M là trung điểm của BB'. Mặt phẳng (MDC') chia khối hộp chữ nhật thành hai khối đa diện, một khối chứa đỉnh C và một khối chứa đỉnh A'. Gọi V 1 , V 2 lần lượt là thể tích hai khối đa diện chứa C và A'. Tính V 1 V 2 .
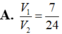
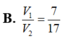
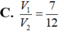
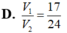
Gọi a, b, c lần lượt là ba kích thước của một khối hộp chữ nhật (H) và V là thể tích của khối hộp chữ nhật (H). Khi đó V được tính bởi công thức:
Đọc tiếp
Gọi a, b, c lần lượt là ba kích thước của một khối hộp chữ nhật (H) và V là thể tích của khối hộp chữ nhật (H). Khi đó V được tính bởi công thức:
![]()
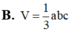
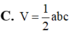
![]()
Cho hình hộp chữ nhật ABCD.A B C D có tổng diện tích của tất cả các mặt là 36, độ dài đường chéo AC bằng 6. Hỏi thể tích của khối hộp lớn nhất là bao nhiêu? A. 8 B.
8
2
C.
16
2
D.
24
3
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A' B' C' D' có tổng diện tích của tất cả các mặt là 36, độ dài đường chéo AC' bằng 6. Hỏi thể tích của khối hộp lớn nhất là bao nhiêu?
A. 8
B. 8 2
C. 16 2
D. 24 3
Nếu một khối hộp chữ nhật có độ dài các đường chéo của các mặt lần lượt là 5 ; 10 , 13 thì thể tích khối hộp chữ nhật đó bằng:
A. 6
B. 5
C. 4
D. 8
Cho khối hộp ABCD.ABCD có đáy là hình chữ nhật, AB
3
AD
7
Hai mặt bên (ABBA) (ADDA) tạo với đáy các góc lần lượt là
45
o
và
60
o
. Tính thể tích V của khối hộp đã cho biết độ dài cạnh bên bằng 1. A. V 3 B. V
7
3...
Đọc tiếp
Cho khối hộp ABCD.A'B'C'D' có đáy là hình chữ nhật, AB = 3 AD= 7 Hai mặt bên (ABB'A) (ADD'A') tạo với đáy các góc lần lượt là 45 o và 60 o . Tính thể tích V của khối hộp đã cho biết độ dài cạnh bên bằng 1.
A. V = 3
B. V = 7 3
C. V = 3
D. V = 7
Tính độ dài đường chéo của hình hộp chữ nhật có ba kích thước là a, b, c
Đọc tiếp
Tính độ dài đường chéo của hình hộp chữ nhật có ba kích thước là a, b, c
![]()
![]()
![]()
![]()
Thể tích của khối hộp chữ nhật có các kích thước lần lượt là a, 2a, 3a bằng. A.
6
a
3
B.
6
a
2
C.
2
a
3
D.
3
a
3
2
5
Đọc tiếp
Thể tích của khối hộp chữ nhật có các kích thước lần lượt là a, 2a, 3a bằng.
A. 6 a 3
B. 6 a 2
C. 2 a 3
D. 3 a 3 2 5



