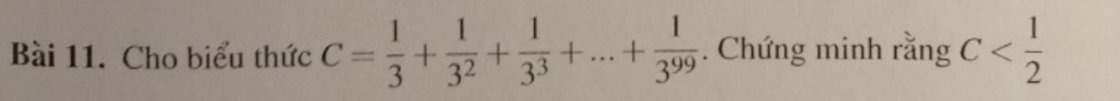\(C=\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{99}}\\ 3C=1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{98}}\)
Xét \(3C-C=1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{9^{98}}-\dfrac{1}{3}-\dfrac{1}{3^2}-\dfrac{1}{3^3}-...-\dfrac{1}{3^{99}}\\ 2C=1-\dfrac{1}{3^{99}}\\ C=\dfrac{1-\dfrac{1}{3^{99}}}{2}=\dfrac{1}{2}-\dfrac{\dfrac{1}{3^{99}}}{2}< \dfrac{1}{2}\left(dpcm\right)\)