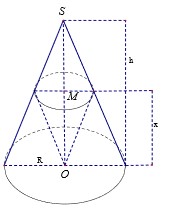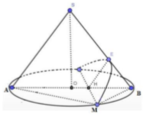
Khi cắt hình nón bởi mặt phẳng song song với đường sinh của hình nón thì ta được thiết diện là một parabol.
Giả sử thiết diện như hình vẽ.
Khi đó ta luôn có A B ⊥ M H
Kẻ HE / /SA trong mặt phẳng (SAB)
Khi đó SA//(HME)
Đặt BH=x(0<x<24), ta có
S A = S O 2 + O A 2 = 16 2 + 12 2 = 20 c m
Xét tam giác AMB vuông tại M có
M H 2 = A H . B H = x 24 - x ⇒ M H = x 24 - x
(hệ thức lượng trong tam giác vuông).
Xét tam giác SAB có HE//SA
⇒ B H A B = H E S E ⇔ H E = x . 20 24 = 5 6 x
Thiết diện parabol có chiều cao H E = 5 6 x và bán kính r=MH=x(24-x)
Diện tích thiết diện là
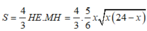
![]()
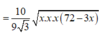
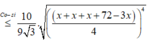
≈ 207 , 8 c m 2
Dấu = xảy ra khi x=72-3x ⇔ x=18(tm)
Vậy diện tích lớn nhất của thiết diện là S ≈ 207 , 8 c m 2
Chọn đáp án D.