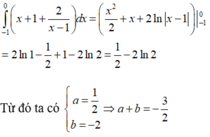Các câu hỏi tương tự
Kết quả của tích phân
∫
-
1
0
x
+
1
+
2
x
-
1
d
x
được viết dưới dạng
a
+
b
ln...
Đọc tiếp
Kết quả của tích phân ∫ - 1 0 x + 1 + 2 x - 1 d x được viết dưới dạng a + b ln 2 với a , b ∈ ℚ . Khi đó a+b bằng:
A. 3 2
B. - 3 2
C. 5 2
D. - 5 2
Tính tích phân
I
∫
-
2
0
x
2
-
x
-
2
x
-
1
d
x
ta được kết quả I a + bln2 + cln3 ( với a, b, c là các số nguyên). Khi đó giá trị...
Đọc tiếp
Tính tích phân I = ∫ - 2 0 x 2 - x - 2 x - 1 d x ta được kết quả I = a + bln2 + cln3 ( với a, b, c là các số nguyên). Khi đó giá trị của biểu thức T = 2 a 3 + 3 b - 4 c là:
A. T = -20.
B. T = 3.
C. T = 22.
D. T = 6.
Giá trị nhỏ nhất của hàm số f(x) = x +1/x trên nửa khoảng [2;+••] A:2 B:5/2 C:0 D:7/2
Cho số phức z thỏa điều kiện
z
+
2
z
+
2
i
. Giá trị nhỏ nhất của biểu thức
P
z
-
1...
Đọc tiếp
Cho số phức z thỏa điều kiện z + 2 = z + 2 i .
Giá trị nhỏ nhất của biểu thức P = z - 1 - 2 i + z - 3 - 4 i + z - 5 - 6 i được viết dưới dạng ( a + b 17 ) 2 với a, b là các hữu tỉ.
Giá trị của a + b là
A. 4
B. 2
C. 7
D. 3
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x)= x^3-3x^2+2 trên đoạn [-1,2] . Tính giá trị biểu thức P= M-2m A. 3√2-3 B. 2√2-5 C. 3√3-5 D. 3√3-3
Cho hàm số: y x3+2mx2+3(m-1)x+2 có đồ thị (C) . Đường thẳng d: y - x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0; -2); B và C. Với M(3;1) giá trị của tham số m để tam giác MBC có diện tích bằng
2
7
là A. m-1 B. m-1 hoặc m4 C. m4 D. Không tồn tại m
Đọc tiếp
Cho hàm số: y = x3+2mx2+3(m-1)x+2 có đồ thị (C) . Đường thẳng d: y= - x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0; -2); B và C. Với M(3;1) giá trị của tham số m để tam giác MBC có diện tích bằng 2 7 là
A. m=-1
B. m=-1 hoặc m=4
C. m=4
D. Không tồn tại m
Hàm số y = ( x + 1 ) 3 (5 - x) có mấy điểm cực trị?
A. 0 B. 1
C. 2 D. 3
Tích phân
∫
x
ln
(
x
+
3
)
d
x
a
+
b
ln
2
+
c
ln
5
với a,b,c là các số hữu tỷ. Giá trị của abc bằng A. -30 B. -10 C. -20 D. -15
Đọc tiếp
Tích phân ∫ x ln ( x + 3 ) d x = a + b ln 2 + c ln 5 với a,b,c là các số hữu tỷ. Giá trị của abc bằng
A. -30
B. -10
C. -20
D. -15
Hoành độ các điểm cực tiểu của hàm số y = x 4 + 3 x 2 + 2 là:
A. x = −1; B. x = 5;
C. x = 0; D. x = 1, x = 2.