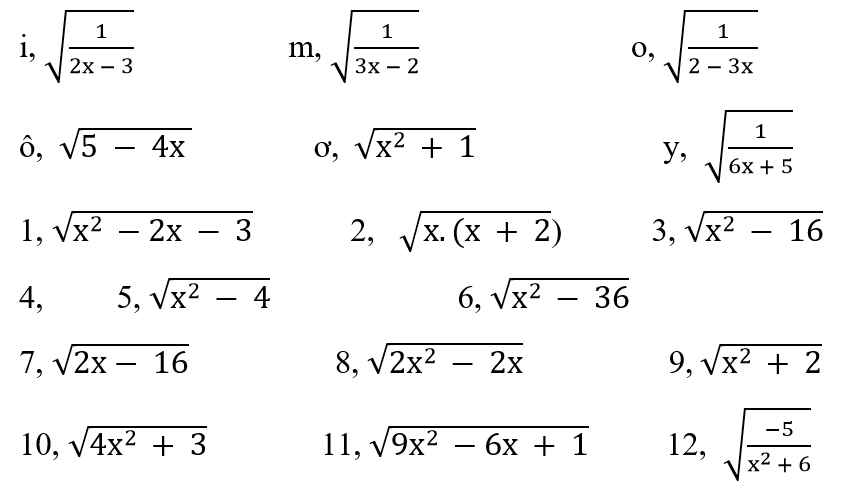Câu 1:
`sqrt(-2/(3-x))` xác định.
`-> 3 - x <= 0`
`-> x >= 3`.
Câu 2:
\(\dfrac{3}{2\sqrt{6}+5}+\dfrac{3}{2\sqrt{6}-5}\)
\(=\dfrac{3\left(2\sqrt{6}-5\right)+3\left(2\sqrt{6}+5\right)}{\left(2\sqrt{6}-5\right)\left(2\sqrt{6}+5\right)}\)
\(=\dfrac{6\sqrt{6}-15+6\sqrt{6}+15}{24-25}\)
\(=-12\sqrt{6}\)
Câu 3:
a) Điều kiện: \(x\ge2\)
\(\sqrt{x-2}+1=4\)
\(\Leftrightarrow\sqrt{x-2}=3\)
\(\Leftrightarrow x-2=9\)
\(\Leftrightarrow x=11\) (nhận)
Vậy phương trình có tập nghiệm là: \(S=\left\{11\right\}.\)
b) \(\sqrt{4x^2}=3\)
\(\Leftrightarrow\sqrt{\left(2x\right)^2}=3\)
\(\Leftrightarrow\left|2x\right|=3\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=3\\2x=-3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\)
Vậy phương trình có tập nghiệm là: \(S=\left\{\dfrac{3}{2};-\dfrac{3}{2}\right\}.\)
Câu 4:
a) \(B=\left[\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}+\dfrac{1}{\sqrt{x}-1}\right]:\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)^2}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)^2}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}.\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}}\)
b) Yêu cầu bài toán: \(\dfrac{\sqrt{x}-1}{\sqrt{x}}=\dfrac{1}{3}\)
\(\Rightarrow3\left(\sqrt{x}-1\right)=\sqrt{x}\)
\(\Leftrightarrow3\sqrt{x}-3=\sqrt{x}\)
\(\Leftrightarrow2\sqrt{x}=3\)
\(\Leftrightarrow\sqrt{x}=\dfrac{3}{2}\)
\(\Leftrightarrow x=\dfrac{9}{4}\) (nhận)
Vậy với \(x=\dfrac{9}{4}\) thì \(B=\dfrac{1}{3}.\)