Các câu hỏi tương tự
Cho a,b,x,y là các số phức thỏa mãn các điều kiện
a
2
-
4
b
16
+
12
i
,
x
2
+
a
x
+
b
+
z
0
,
y
2
+
a
y
+
b
+
z
0
,
x...
Đọc tiếp
Cho a,b,x,y là các số phức thỏa mãn các điều kiện a 2 - 4 b = 16 + 12 i , x 2 + a x + b + z = 0 , y 2 + a y + b + z = 0 , x - y = 2 3 . Gọi M,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của z . Tính M+m.
![]()
![]()
![]()
![]()
Các số thực a,b,c,x,y,z thỏa mãn
a
2
+
b
2
+
c
2
-
2
a
+
4
c
+
4
0
và
x
2
+
y
2
+
z
2
-
4
x
+
4
y
+
4...
Đọc tiếp
Các số thực a,b,c,x,y,z thỏa mãn a 2 + b 2 + c 2 - 2 a + 4 c + 4 = 0 và x 2 + y 2 + z 2 - 4 x + 4 y + 4 = 0 . Tìm GTLN của S = a - x 2 + b - y 2 + z - c 2 .
![]()
![]()
![]()
![]()
Cho đồ thị
C
.
y
a
x
+
b
x
+
2
cắt Oy tại điểm
A
0
;
2
và tiếp tuyến tại A của
C
có hệ số góc
k
-
1
. Khi đó...
Đọc tiếp
Cho đồ thị C . y = a x + b x + 2 cắt Oy tại điểm A 0 ; 2 và tiếp tuyến tại A của C có hệ số góc k = - 1 . Khi đó a 2 + b 2 bằng
A.17
B.16
C.10
D.13
Diện tích hình phẳng giới hạn bởi
a
y
x
2
và
a
x
y
2
là: A.
-
a
3
3
B.
a
3
3
C.
a
2
D.
-
a
2
Đọc tiếp
Diện tích hình phẳng giới hạn bởi a y = x 2 và a x = y 2 là:
A. - a 3 3
B. a 3 3
C. a 2
D. - a 2
Biết đồ thị hàm số
y
x
3
+
a
x
2
+
b
x
+
c
(với a, b, c là các số thực đi qua điểm (1;0) và có điểm cực trị (-2; 0)). Tính giá trị biểu thức
T
a
2
+
b
2
+
c
2
+
2
. A. 18 B. 7 C. 9 D....
Đọc tiếp
Biết đồ thị hàm số y = x 3 + a x 2 + b x + c (với a, b, c là các số thực đi qua điểm (1;0) và có điểm cực trị (-2; 0)). Tính giá trị biểu thức T = a 2 + b 2 + c 2 + 2 .
A. 18
B. 7
C. 9
D. 27
Tìm các giá trị của a (a0) để hệ phương trình
a
x
+
a
y
1
2
x
+
y...
Đọc tiếp
Tìm các giá trị của a (a>0) để hệ phương trình a x + a y = 1 2 x + y = b 2 - b + 1 có nghiệm ∀ b ∈ 0 ; 1
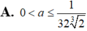
![]()
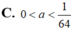
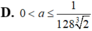
Biết rằng đồ thị hàm số
y
(
3
a
2
-
1
)
x
3
-
(
b
3
+
1
)
x
2
+
3
c
2
x
+
4
d
có hai điểm cực trị là (1;-7), (2:-8). Hãy xác định tổng M...
Đọc tiếp
Biết rằng đồ thị hàm số y = ( 3 a 2 - 1 ) x 3 - ( b 3 + 1 ) x 2 + 3 c 2 x + 4 d có hai điểm cực trị là (1;-7), (2:-8). Hãy xác định tổng M= a 2 + b 2 + c 2 + d 2 .
A. -18
B. 18
C. 15
D. 8
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a,
S
A
⊥
(
A
B
C
D
)
. Biết
S
A
y
;
M
∈
A
D
;
A...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, S A ⊥ ( A B C D ) . Biết S A = y ; M ∈ A D ; A M = x ; x 2 + y 2 = a 2 . Khi đó giá trị lớn nhất của V S . A B C M là:
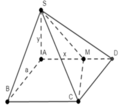
A. a 3 3 4
B. a 3 8
C. a 3 3 2
D. a 3 3 8
Biểu thức tổng quát của hàm số có đò thị như hình 1.6 là:A. y a
x
2
+ bx + c với a ≠ 0B. y a
x
3
+ cx + d với a 0C. y a
x
3
+ b
x
2
+ cx + d với a 0 và
b
2
- 3ac 0D. y
x
3
Đọc tiếp
Biểu thức tổng quát của hàm số có đò thị như hình 1.6 là:
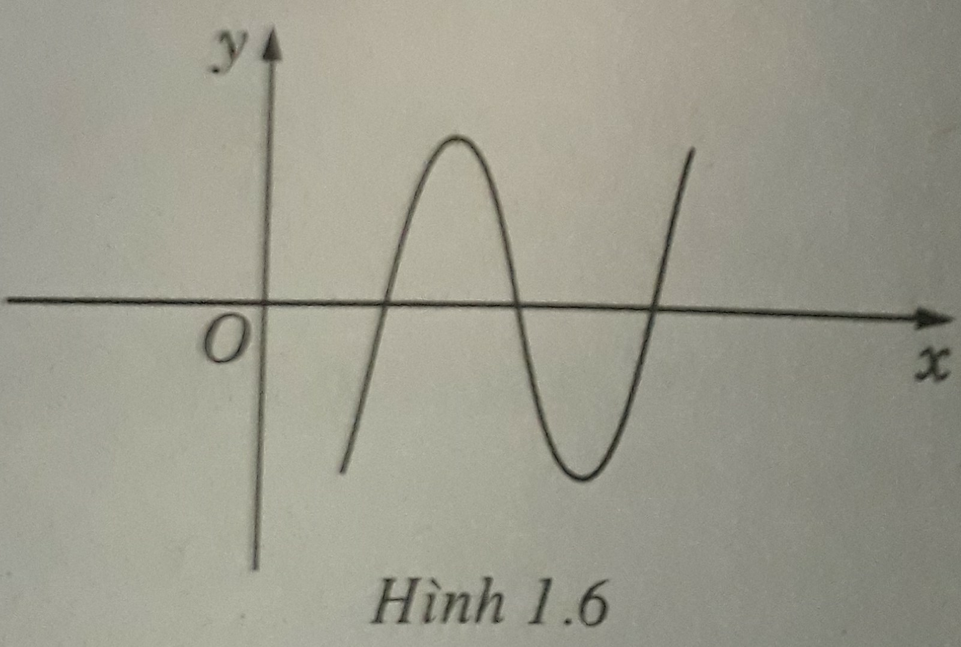
A. y = a x 2 + bx + c với a ≠ 0
B. y = a x 3 + cx + d với a < 0
C. y = a x 3 + b x 2 + cx + d với a > 0 và b 2 - 3ac > 0
D. y = x 3


