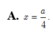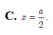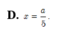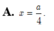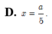Đáp án D
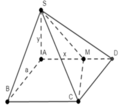
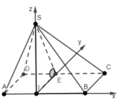
Ta có: S A B C M = A M + B C 2 . A B = a ( x + a ) 2 (đvdt)
⇒ V S . A B C M = 1 3 . S A . S A B C M = a ( x + a ) a 2 - x 2 6 (đvtt).
Đặt f ( x ) = ( x + a ) a 2 - x 2
![]()
Xét phương trình f ' ( x ) = 0 ⇒ x = a 2
⇒ f ( x ) đạt giá trị lớn nhất khi x = a 2
Từ đó suy ra V S . A B C M m a x = a 3 3 8 (đvtt).