Bài 2:
a: Xét ΔDAB có M,N lần lượt là trung điểm của DA,DB
=>MN là đường trung bình của ΔDAB
=>MN//AB và \(MN=\frac{AB}{2}\)
Xét ΔBDC có N,K lần lượt là trung điểm của BD,BC
=>NK là đường trung bình của ΔBDC
=>NK//DC và \(NK=\frac{DC}{2}\)
Ta có: MN+NK>=MK
=>\(\frac12\left(AB+CD\right)\ge MK\)
b: AB//CD
mà MN//AB
nên MN//CD
mà NK//DC
và MN,NK có điểm chung là N
nên M,N,K thẳng hàng
Xét ΔCAB có I,K lần lượt là trung điểm của CA,CB
=>IK là đường trung bình của ΔCAB
=>IK//AB và \(IK=\frac{AB}{2}\)
Ta có: IK//AB
MK//AB
mà IK,MK có điểm chung là K
nên I,K,M thẳng hàng
=>M,N,I,K thẳng hàng
NK=MN+NK
=>\(NK=\frac{AB}{2}+\frac{CD}{2}=\frac12\left(AB+CD\right)\)
Ta có; MN+NI+IK=MK
=>\(\frac12AB+\frac12AB+NI=\frac12\left(AB+CD\right)\)
=>\(NI=\frac12\left(AB+CD-2AB\right)=\frac12\left(CD-AB\right)\)
Bài 5:
a: Gọi K là giao điểm của MB và DC
Xét ΔMAB vuông tại A và ΔMDK vuông tại D có
MA=MD
\(\hat{AMB}=\hat{DMK}\) (hai góc đối đỉnh)
Do đó: ΔMAB=ΔMDK
=>AB=DK và MB=MK
Xét ΔCBK có
CM là đường cao
CM là đường trung tuyến
Do đó; ΔCBK cân tại C
=>CK=CB
=>CB=CD+DK=CD+BA
b: ΔCBK cân tại C
mà CM là đường cao
nên CM là phân giác của góc BCK
Xét ΔCDM vuông tại D và ΔCHM vuông tại H có
CM chung
\(\hat{DCM}=\hat{HCM}\)
Do đó: ΔCDM=ΔCHM
=>CH=CD và MH=MD
=>CM là đường trung trực của HD
=>CM⊥HD
mà CM⊥MB
nên HD//MB
=>MBHD là hình thang
Bài 4:
a: Gọi K là giao điểm của AM và DC
Xét ΔMAB và ΔMKC có
\(\hat{MBA}=\hat{MCK}\) (hai góc so le trong, AB//CK)
MB=MC
\(\hat{BMA}=\hat{CMK}\) (hai góc đối đỉnh)
Do đó: ΔMAB=ΔMKC
=>MA=MK và AB=KC
Xét ΔDMK vuông tại M và ΔDMA vuông tại M có
DM chung
MK=MA
Do đó: ΔDMK=ΔDMA
=>DK=DA
=>DA=DC+CK
mà CK=AB
nên DA=DC+AB
b: ΔDMK=ΔDMA
=>\(\hat{MDK}=\hat{MDA}\)
=>DM là phân giác của góc ADK
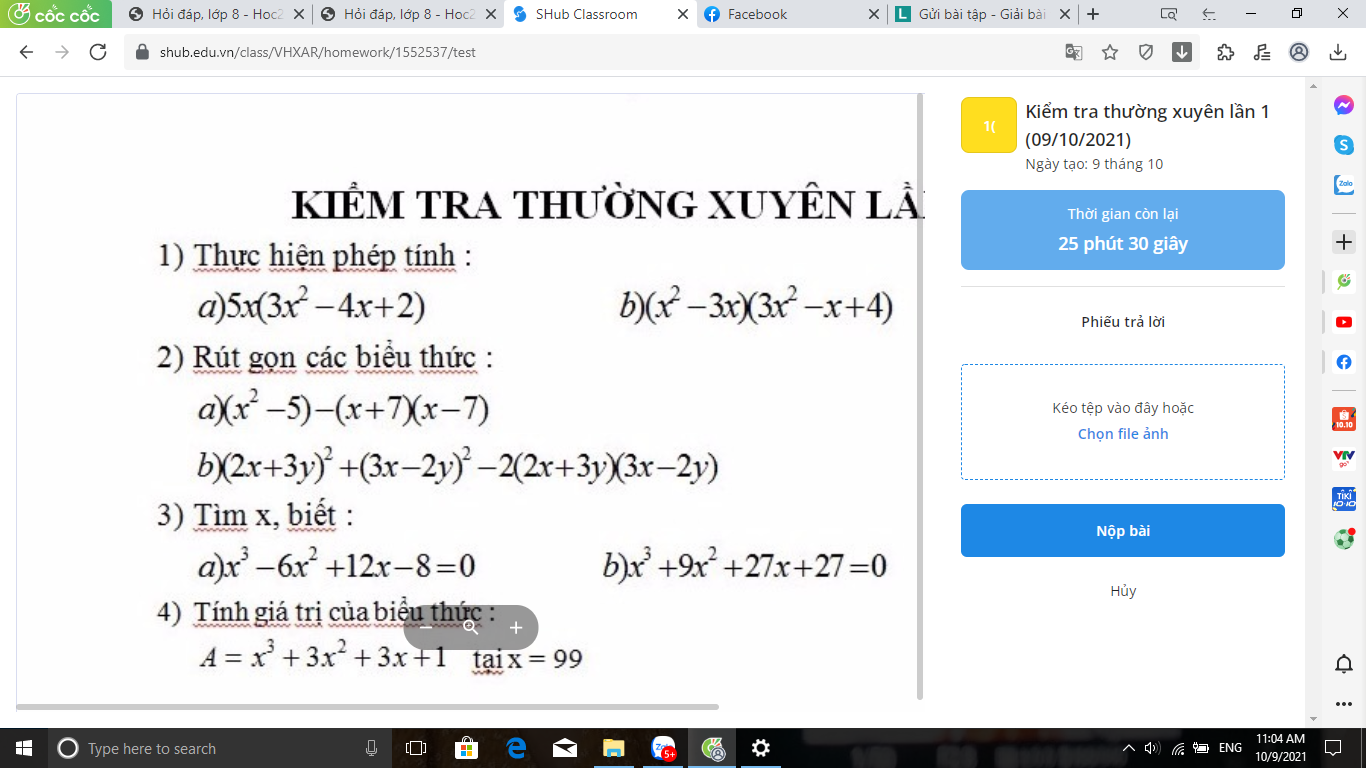
giúp tớ vớiiiii
giúp mình vớiiiii ạ 
