Đáp án C
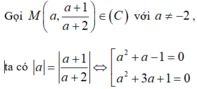
Phương trình có 4 nghiệm nên trên đồ thị có 4 điểm cách đều hai trục tọa độ
Đáp án C
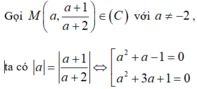
Phương trình có 4 nghiệm nên trên đồ thị có 4 điểm cách đều hai trục tọa độ
Cho đồ thị (C) của hàm số y = x 2 - 3 x + 3 - x + 1 . Tìm điểm M trên đồ thị (C) sao cho M cách đều hai trục tọa độ
A.![]()
B. ![]()
C. ![]()
D. ![]()
Tọa độ điểm M thuộc đồ thị (C) của hàm số y = x + 3 x - 1 cách đều hai trục tọa độ là
A.![]()
B. ![]()
C. ![]()
D. ![]()
Có bao nhiêu điểm M thuộc đồ thị (C) của hàm số 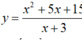 cách đều hai trục tọa độ ?
cách đều hai trục tọa độ ?
A. 2
B. Có vô số điểm M thỏa yêu cầu.
C. 1.
D. Không có điểm M thỏa yêu cầu.
Cho đồ thị (C) của hàm số y = x - 3 x + 1 Điểm M nào dưới đây thuộc đồ thị (C) và cách đều hai trục tọa độ
A.![]()
B.![]()
C.![]()
D. ![]()
Cho (C) là đồ thị của hàm số y = x - 3 x + 1 Biết rằng, chỉ có hai điểm thuộc đồ thị (C) cách đều hai điểm A(2;0) và B(0;-2). Gọi các điểm đó lần lượt là M và N. Tìm tọa độ trung điểm I của đoạn thẳng MN.
A. I(-1;1)
B.I(0;-3/2)
C.I(0;3/2)
D. I(-2;2)
Cho (C) là đồ thị của hàm số y = x - 3 x + 1 Biết rằng chỉ có đúng hai điểm thuộc đồ thị (C) cách đều hai trục tọa độ. Gọi các điểm đó lần lượt là M và N. Tính độ dài đoạn thẳng MN.
A.![]()
B. MN = 3
C. ![]()
D. ![]()
Cho hàm số y = x − 1 x + 1 có đồ thị (C), điểm M di động trên (C). Gọi d là tổng khoảng cách từ M đến hai trục tọa độ. Khi đó giá trị nhỏ nhất của d là:
A. 207 250 .
B. 2 − 1.
C. 2 2 − 1.
D. 2 2 − 2 .
Tọa độ giao điểm của đồ thị các hàm số:
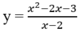
và y = x + 1 là:
A. (2; 2); B. (2; -3);
C(-1; 0); D. (3; 1).
Tọa độ điểm M thuộc đồ thị (C) của hàm số y = x + 2 x - 2 cách đều hai đường tiệm cận của (C) là
A.![]()
B. ![]()
C. 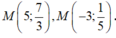
D. ![]()