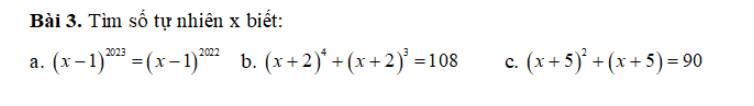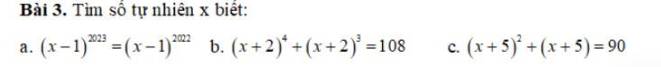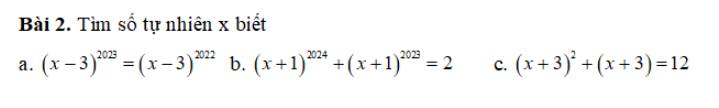a: \(\left(x-1\right)^{2023}=\left(x-1\right)^{2022}\)
=>\(\left(x-1\right)^{2023}-\left(x-1\right)^{2022}=0\)
=>\(\left(x-1\right)^{2022}\left(x-1-1\right)=0\)
=>\(\left(x-1\right)^{2022}\cdot\left(x-2\right)=0\)
=>\(\left[{}\begin{matrix}\left(x-1\right)^{2022}=0\\x-2=0\end{matrix}\right.0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
b: Đặt \(\left(x+2\right)^4+\left(x+2\right)^3=108\)
Đặt x+2=a
Phương trình sẽ trở thành: \(a^4+a^3=108\)
=>\(a^4-3a^3+4a^3-108=0\)
=>\(a^3\left(a-3\right)+4\left(a-3\right)\left(a^2+3a+9\right)=0\)
=>\(\left(a-3\right)\left(a^3+4a^2+12a+36\right)=0\)
=>\(\left[{}\begin{matrix}a-3=0\\a^3+4a^2+12a+36=0\left(loại\right)\end{matrix}\right.\)
=>a-3=0
=>a=3
=>x+2=3
=>x=1
c: \(\left(x+5\right)^2+\left(x+5\right)=90\)
=>\(x^2+10x+25+x+5-90=0\)
=>x^2+11x-60=0
=>(x+15)(x-4)=0
=>\(\left[{}\begin{matrix}x=-15\\x=4\end{matrix}\right.\)