Các câu hỏi tương tự
Cho hàm số y f (x) liên tục trên R có đồ thị như hình vẽ. Biết trên
(
-
∞
;
-
3
)
∪
(
2
;
+
∞
)
t
h
ì
f
(
x
)
0
. Số nghiệm nguyên thuộc (-10; 10) của bất phương trình
[
f
(
x
)...
Đọc tiếp
Cho hàm số y = f (x) liên tục trên R có đồ thị như hình vẽ.
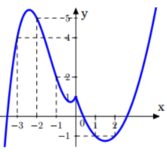
Biết trên ( - ∞ ; - 3 ) ∪ ( 2 ; + ∞ ) t h ì f ' ( x ) > 0 . Số nghiệm nguyên thuộc (-10; 10) của bất phương trình [ f ( x ) + x - 1 ] ( x 2 - x - 6 ) > 0 là
A. 9
B. 10
C. 8
D. 7
Cho hàm số yf(x) liên tục trên đoạn [a;c] và abc. Biết
∫
a
b
f
(
x
)
d
x
-
10
,
∫
c
a
f
(
x
)
d
x
-
5
. Tính
∫
c
b
f
(
x
)
d
x
A...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên đoạn [a;c] và a<b<c. Biết ∫ a b f ( x ) d x = - 10 , ∫ c a f ( x ) d x = - 5 . Tính ∫ c b f ( x ) d x
A. 15
B. -15
C. -5
D. 5
Cho hàm số
f
(
x
)
(
1
-
x
+
x
2
)
10
Giá trị đạo hàm cấp 5 của hàm số tại
x
o
1
là A. 34848 B. 30240 C. 125240 D. 174240
Đọc tiếp
Cho hàm số f ( x ) = ( 1 - x + x 2 ) 10 Giá trị đạo hàm cấp 5 của hàm số tại x o = 1 là
A. 34848
B. 30240
C. 125240
D. 174240
Cho
a
,
b
là các số thực và hàm số
f
(
x
)
a
log
2019
(
x
2
+
1
+
x
)
+
b
sin
x
.
c
os
(
2018
x
)...
Đọc tiếp
Cho a , b là các số thực và hàm số f ( x ) = a log 2019 ( x 2 + 1 + x ) + b sin x . c os ( 2018 x ) + 6 . Biết f ( 2018 ln 2019 ) = 10 . Tính P = f − 2019 ln 2018 .
A. P = 4.
B. P = 2.
C. P = − 2.
D. P = 10.
Cho hàm số f(x) có đạo hàm f(x) thỏa mãn các đẳng thức
∫
0
1
(
2
x
-
1
)
f
(
x
)
d
x
10
,
...
Đọc tiếp
Cho hàm số f(x) có đạo hàm f'(x) thỏa mãn các đẳng thức ∫ 0 1 ( 2 x - 1 ) f ' ( x ) d x = 10 , f ( 1 ) + f ( 8 ) = 0 . Tính I = ∫ 0 1 f ( x ) d x .
A. I = 2.
B. I = 1.
C. I = -1.
D. I = -2.
Cho hàm số f(x)
1
+
x
+
(
a
2
-
2
a
-
2
)
a
4
-
10
a
2
+
10
-
x
Trong đó a là tham số. Có bao nhiêu giá trị a để f là hàm số chẵn A. 2. B. 1. C. 4. ...
Đọc tiếp
Cho hàm số f(x)= 1 + x + ( a 2 - 2 a - 2 ) a 4 - 10 a 2 + 10 - x Trong đó a là tham số. Có bao nhiêu giá trị a để f là hàm số chẵn
A. 2.
B. 1.
C. 4.
D. 3
Cho hàm số
y
2
x
+
1
x
+
1
có đồ thị (C) và đường thẳng d:yx+m. Giá trị của tham số m để d cắt (C) tại hai điểm phân biệt A, B sao cho
A
B
10...
Đọc tiếp
Cho hàm số y = 2 x + 1 x + 1 có đồ thị (C) và đường thẳng d:y=x+m. Giá trị của tham số m để d cắt (C) tại hai điểm phân biệt A, B sao cho A B = 10 là:
A.m=-1 hoặc m=6 hoặc m=7
B. 0 ≤ m ≤ 5
C.m=0 hoặc m=6
D.m=0
Cho hàm sốf (x) có đạo hàm trên [1;4] và f(1), f(4) 10.Giá trị của
I
∫
1
4
f
(
x
)
d
x
là A. I 12 B. I 48 C. I 8 D. I 3
Đọc tiếp
Cho hàm sốf (x) có đạo hàm trên [1;4] và f(1), f(4) = 10.Giá trị của I = ∫ 1 4 f ' ( x ) d x là
A. I = 12
B. I = 48
C. I = 8
D. I = 3
Cho hàm số f(x) có
f
(
x
)
(
x
+
1
)
4
(
x
-
2
)
3
(
2
x
+
3
)
7
(
x
-
1
)
10
. Tìm cực trị f(x) A. 3 B. 2 C. 1 D. 4
Đọc tiếp
Cho hàm số f(x) có f ( x ) = ( x + 1 ) 4 ( x - 2 ) 3 ( 2 x + 3 ) 7 ( x - 1 ) 10 . Tìm cực trị f(x)
A. 3
B. 2
C. 1
D. 4
Tìm nguyên hàm của hàm số
f
(
x
)
2008
+
ln
2
x
x
có dạng
F
(
x
)
a
ln
x
+
ln
x
3
b
+
C
. Khi đó tổng S a + b là? A. 2012 B. 2010 C. 2009 D. 2011
Đọc tiếp
Tìm nguyên hàm của hàm số f ( x ) = 2008 + ln 2 x x có
dạng F ( x ) = a ln x + ln x 3 b + C . Khi đó tổng S
= a + b là?
A. 2012
B. 2010
C. 2009
D. 2011



