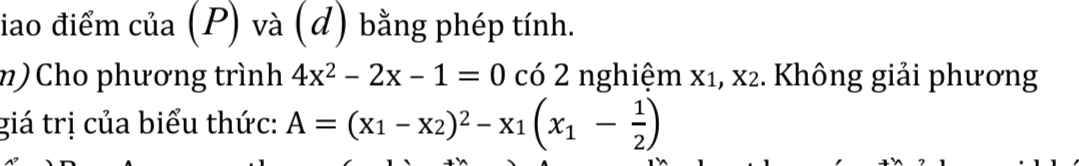Ta có : \(\Delta'=b'^2-ac=\left(-1\right)^2-4.\left(-1\right)=5>0\)
⇒ Phương trình có hai nghiệm phân biệt.
Theo định lí Vi-ét : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-\dfrac{-2}{4}=\dfrac{1}{2}\\x_1x_2=\dfrac{c}{a}=-\dfrac{1}{4}\end{matrix}\right.\)
Theo đề bài : \(A=\left(x_1-x_2\right)^2-x_1\left(x_1-\dfrac{1}{2}\right)\)
\(=x_1^2-2x_1x_2+x_2^2-x_1\left[x_1-\left(x_1+x_2\right)\right]\)
\(=\left(x_1^2+2x_1x_2+x_2^2\right)-4x_1x_2+x_1x_2\)
\(=\left(x_1+x_2\right)^2-3x_1x_2\)
\(\Rightarrow A=\left(\dfrac{1}{2}\right)^2-3\cdot\left(-\dfrac{1}{4}\right)=1\)
Vậy : \(A=1.\)