Đáp án D
Dựa vào hình tứ diện đều và khái niệm mặt phẳng đối xứng của khối đa diện.
Mặt phẳng tạo bởi hai đỉnh bất kì và trung điểm của cạnh đối là mặt phẳng đối xứng của tứ diện đều.
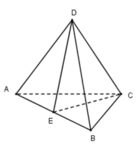
Tứ diện đều có 4 đỉnh. Vậy có C 4 2 = 6 mặt phẳng đối xứng.
Đáp án D
Dựa vào hình tứ diện đều và khái niệm mặt phẳng đối xứng của khối đa diện.
Mặt phẳng tạo bởi hai đỉnh bất kì và trung điểm của cạnh đối là mặt phẳng đối xứng của tứ diện đều.

Tứ diện đều có 4 đỉnh. Vậy có C 4 2 = 6 mặt phẳng đối xứng.
Hình tứ diện đều có bao nhiêu mặt phẳng đối xứng?
A. 6
B. 4
C. 9
D. 3
Hình tứ diện đều có bao nhiêu mặt phẳng đối xứng?
A. 8
B. 6
C. Vô số
D. 14
Hình tứ diện đều có bao nhiêu mặt phẳng đối xứng?
A. 6.
B. 9
C. 3.
D. 4.
Hỏi hình tạo bởi 6 đỉnh là 6 trung điểm của các cạnh một tứ diện đều có bao nhiêu mặt phẳng đối xứng?
A. 6
B. 3
C. 4
D. 9
Số mặt phẳng đối xứng của hình tứ diện đều là bao nhiêu?
A. 4
B. 5
C. 9
D. 3
Tứ diện đều có bao nhiêu mặt phẳng đối xứng?
A.2
B.3
C.6
D.9
Khối tứ diện đều có bao nhiêu mặt phẳng đối xứng
A. 3
B. 4
C. 6
D. 9
Tứ diện đều có tất cả bao nhiêu mặt phẳng đối xứng?
A. 3
B. 4
C. 6.
D. 9.
Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng?
A. Một
B. Hai
C. Bốn
D. Ba