Các câu hỏi tương tự
Cho hình cầu (S) tâm O, bán kính R. Hình cầu (S) ngoại tiếp một hình trụ tròn xoay (T) có đường cao bằng đường kính đáy và hình cầu (S) lại nội tiếp trong một hình nón tròn xoay (N) có góc ở đỉnh bằng
60
0
. Tính tỉ số thể tích của hình trụ (T) và hình nón (T) .
A
.
V
T
V
N
2...
Đọc tiếp
Cho hình cầu (S) tâm O, bán kính R. Hình cầu (S) ngoại tiếp một hình trụ tròn xoay (T) có đường cao bằng đường kính đáy và hình cầu (S) lại nội tiếp trong một hình nón tròn xoay (N) có góc ở đỉnh bằng 60 0 . Tính tỉ số thể tích của hình trụ (T) và hình nón (T) .
A . V T V N = 2 6
B . V T V N = 2 3
C . V T V N = 3 2
D. Đáp án khác
Tính thể tích khối tròn xoay sinh ra khi quay hình phẳng dưới đây quanh cạnh có độ dài bằng 14 của nó.
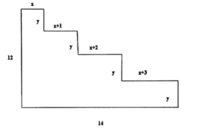
A. 1005 π
B. 720 π
C. 1431 π
D. 1422 π
Trong không gian, cho hình chữ nhật ABCD có AB 2, AD 3. Đường thẳng d nằm trong mặt phẳng (ABCD), không có điểm chung với ABCD, song song với cạnh AB và cách AB một khoảng bằng 1. Tính thể tích V của khối tròn xoay, nhận được khi quay hình chữ nhật ABCD quanh trục d. A. V 17
π
B. V 5
π
C. V 15
π
D. 30
π
Đọc tiếp
Trong không gian, cho hình chữ nhật ABCD có AB = 2, AD = 3. Đường thẳng d nằm trong mặt phẳng (ABCD), không có điểm chung với ABCD, song song với cạnh AB và cách AB một khoảng bằng 1. Tính thể tích V của khối tròn xoay, nhận được khi quay hình chữ nhật ABCD quanh trục d.
A. V = 17 π
B. V = 5 π
C. V = 15 π
D. 30 π
Cho hình chữ nhật ABCD có AB3AD Quay hình chữ nhật ABCD lần lượt quanh AD và AB ta thu được hai hình trụ tròn xoay tương ứng có thể tích
V
1
,
V
2
Hỏi hệ thức nào sau đây là đúng?AD A.
V
2
3
V
1
Đọc tiếp
Cho hình chữ nhật ABCD có AB=3AD Quay hình chữ nhật ABCD lần lượt quanh AD và AB ta thu được hai hình trụ tròn xoay tương ứng có thể tích V 1 , V 2 Hỏi hệ thức nào sau đây là đúng?AD
A. V 2 = 3 V 1
![]()
![]()
![]()
Cho tam giác ABC vuông tại B có AC2a, BCa khi quay tam giác ABC quay quanh cạnh góc vuông AB thì đường gấp khúc ABC tạo thành một hình nón tròn xoay có diện tích xung quanh bằng
Đọc tiếp
Cho tam giác ABC vuông tại B có AC=2a, BC=a khi quay tam giác ABC quay quanh cạnh góc vuông AB thì đường gấp khúc ABC tạo thành một hình nón tròn xoay có diện tích xung quanh bằng
![]()
![]()
![]()
![]()
Trong mặt phẳng (P) cho hình (H) ghép bởi hai hình bình hành có chung cạnh XY như hình vẽ bên. Thể tích V của vật thể tròn xoay sinh ra bởi hình (H) khi quay mặt phẳng (P) xung quanh trục XY là:
Đọc tiếp
Trong mặt phẳng (P) cho hình (H) ghép bởi hai hình bình hành có chung cạnh XY như hình vẽ bên. Thể tích V của vật thể tròn xoay sinh ra bởi hình (H) khi quay mặt phẳng (P) xung quanh trục XY là:
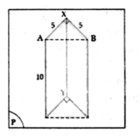
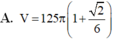
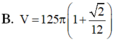
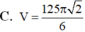
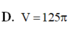
Cho hình thang cân ABCD có các cạnh đáy và cạnh bên ADBC2a Tính theo a thể tích V của khối tròn xoay thu được khi quay hình thang cân ABCD quanh trục đối xứng của nó.
Đọc tiếp
Cho hình thang cân ABCD có các cạnh đáy ![]() và cạnh bên AD=BC=2a Tính theo a thể tích V của khối tròn xoay thu được khi quay hình thang cân ABCD quanh trục đối xứng của nó.
và cạnh bên AD=BC=2a Tính theo a thể tích V của khối tròn xoay thu được khi quay hình thang cân ABCD quanh trục đối xứng của nó.
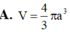
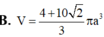
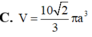
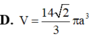
Hình chữ nhật ABCD có AB 4, AD 2. Gọi M và N lần lượt là trung điểm của AB và CD. Cho hình chữ nhật quay quanh MN ta được một khối tròn xoay có thể tích V bằng
Đọc tiếp
Hình chữ nhật ABCD có AB = 4, AD = 2. Gọi M và N lần lượt là trung điểm của AB và CD. Cho hình chữ nhật quay quanh MN ta được một khối tròn xoay có thể tích V bằng
![]()
![]()
![]()
![]()
Cho mô hình (như hình vẽ) với tam giác EFB vuông tại B, cạnh FB a ,
E
F
B
^
30
0
và tứ giác ABCD là hình vuông. Tính thể tích V của vật thể tròn xoay được tạo thành khi quay mô hình quanh cạnh AF A.
4
3
a
3
B. ...
Đọc tiếp
Cho mô hình (như hình vẽ) với tam giác EFB vuông tại B, cạnh FB = a , E F B ^ = 30 0 và tứ giác ABCD là hình vuông. Tính thể tích V của vật thể tròn xoay được tạo thành khi quay mô hình quanh cạnh AF
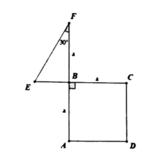
A. 4 3 a 3
B. 10 9 a 3
C. 4 3 πa 3
D. 10 9 πa 3



